I've reproduced Run11 500GeV tranverse pp trigger data, with Steve's calibration "FmsCorrD90q5.txt" and asymmetric shower shower funtion implemented.

 

1) luminosity ratio:

Pion candidates were divided into 6 energy bins with pseudorapidity integrated from (2.5,4.1). I used an energy dependent

mass window in selecting pions. Center of the window was determined by a fit to Gaussian function,window width = 0.1

GeV.

energy bins : 50, 60, 70, 80, 90, 100 GeV

   

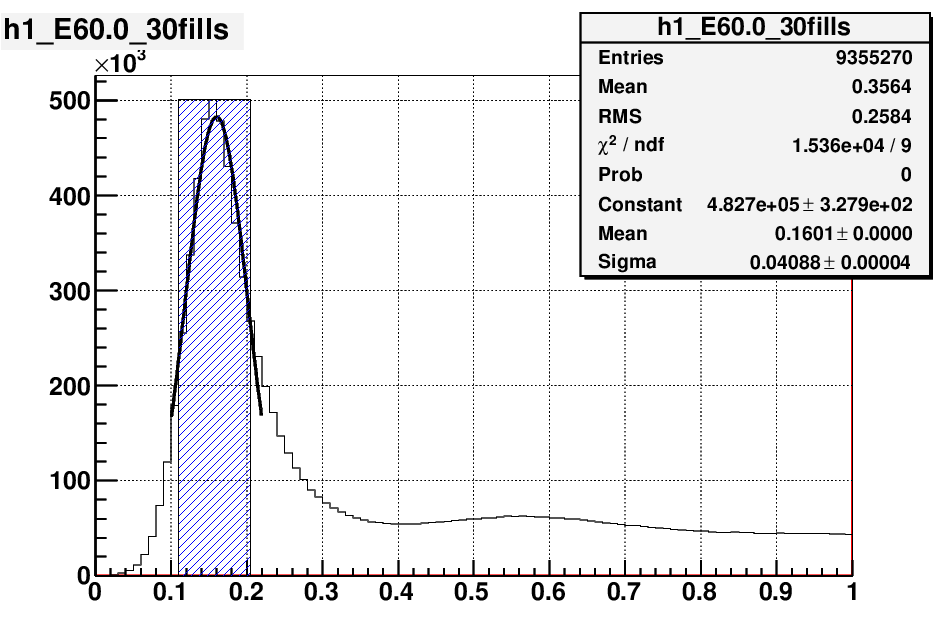
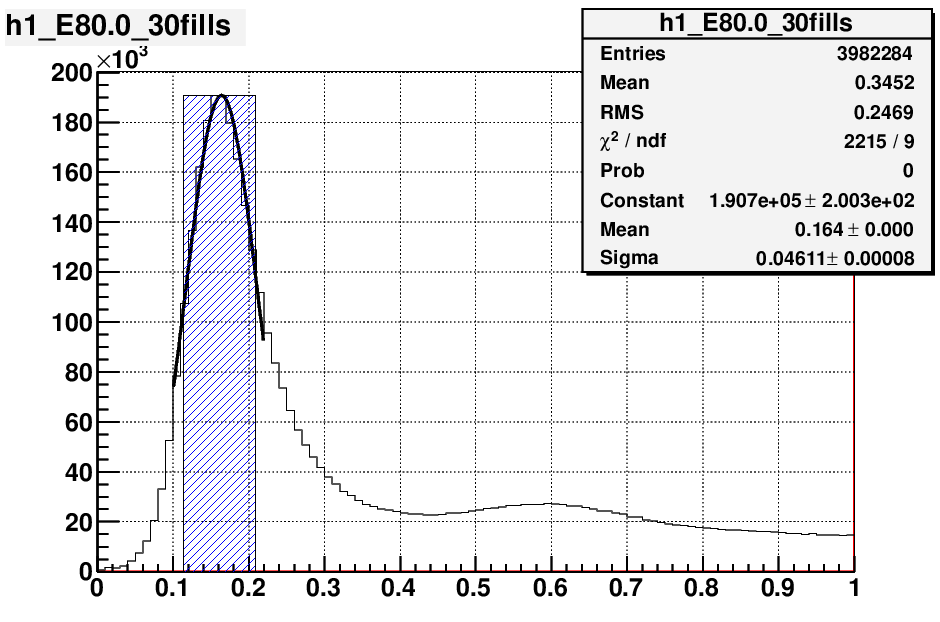
                                     fig.1 a)                                                                                                                      fig. 1 b)

A linear fit was applied to the raw yield asymmetry vs cos(phi) for each of these 6 energy bins, and the average value of the intercept was calculated.

     

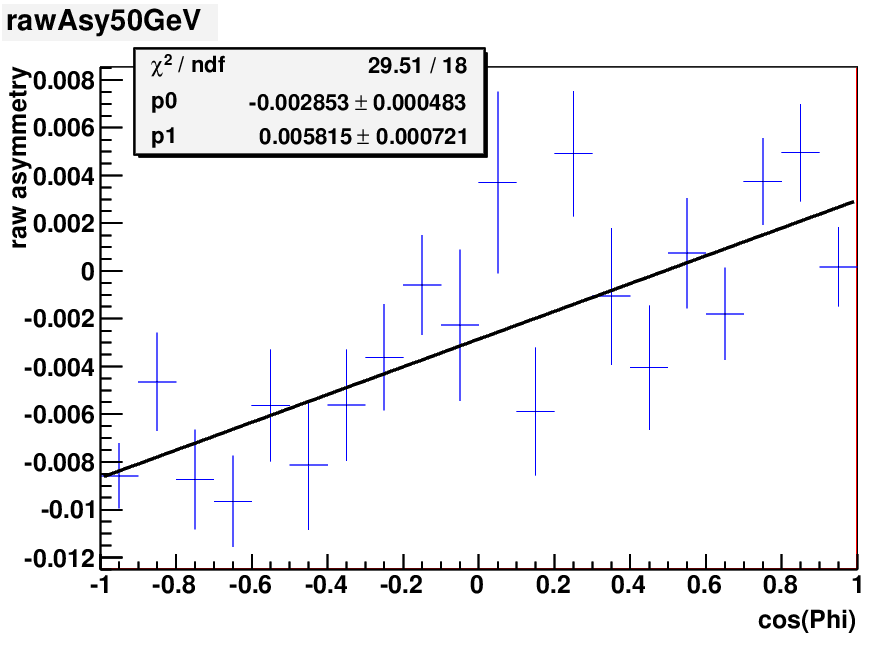
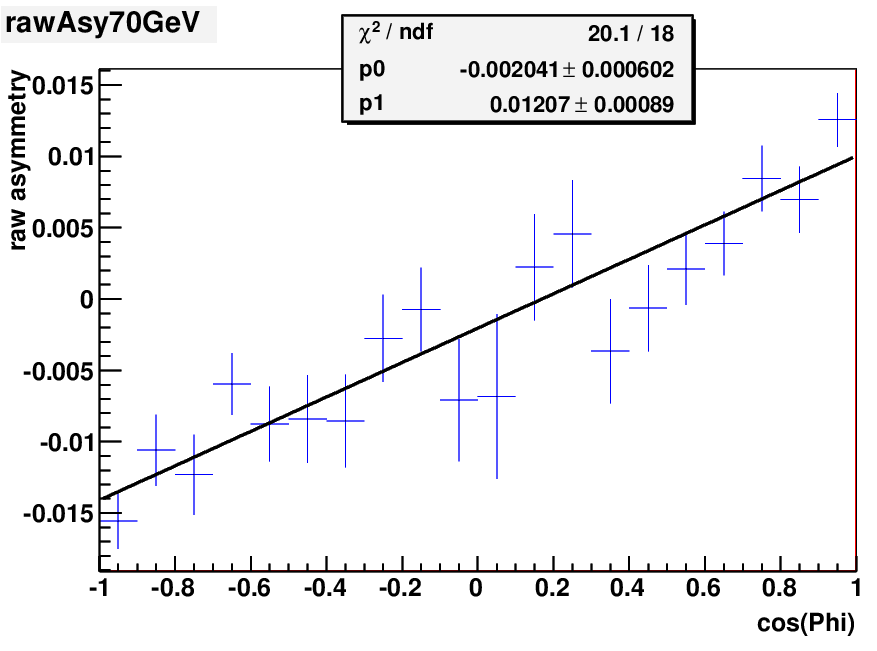
                                             fig. 2 a).                                                                                                                fig. 2 b)

Luminosity ratio = ( L_up - L_down ) / ( L_up + L_down ) = ave. intercept / ave. polarization.

Average polaization = 51.6% +/- 6.7% --> luminosity ratio = -0.39% +/- 0.12%. Steve's result is -0.31% +/- 0.05%

 

2). A_N vs E

Then the raw asymmetry of each energy bin was re-fitted with fixed intercept = 0.39% *51.6% = 0.201%

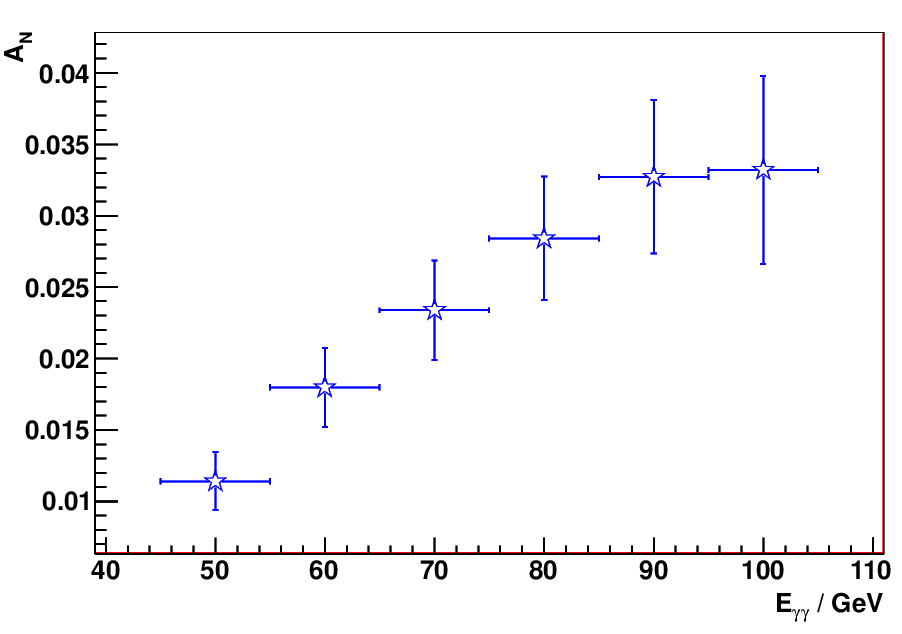
                                                fig. 3

3) A_N vs pT for different energy (x_F)

energy bin = 50, 75, 100 GeV           

x_F ~ (0.15,0.25) , (0.25, 0.35), (0.35, 0.45)

pT bin for 50 GeV:  2.0, 2.5, 3.0, 3.5, 4.0, 4.75, 5.75, 6.75 GeV

pT bin for 75 GeV:  2.5, 3.0, 3.5, 4.0, 4.75, 5.75, 6.75, 7.75 GeV

pT bin for 100 GeV:  3.0, 3.5, 4.0, 4.75, 5.75, 6.75, 7.75 GeV

Same as above, I used a varying energy window for each (pT, xF) bin. e.g:

 

 

                 fig.4 M_rr with E = 75 GeV, pT = 2.5 GeV                                                                 fig.5 M_rr with E = 75 GeV, pT = 3.0 GeV

 

For each (x_F, pT) bin, a linear fit to raw yield vs cos(phi) was applied, with intercept being fixed at the same value as above.

      

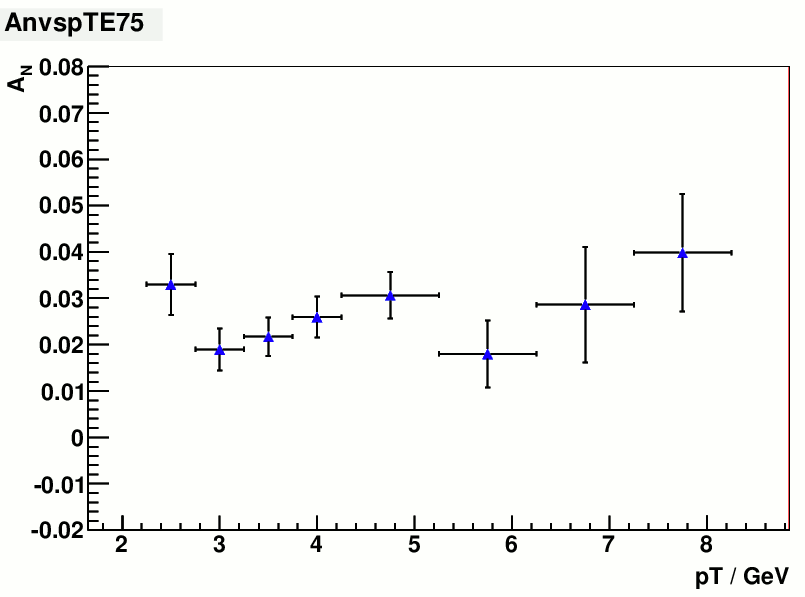
                         fig. 6 A_N vs pT for 0.15 < x_F < 0.25                                                                           fig. 7 A_N vs pT for 0.25 < x_F < 0.35

 

                                 fig. 7 A_N vs pT for 0.35 < x_F < 0.45

Link to Steve's CIPANP talk

 

 

I am also looking into the possibility of constructing the backgroud shape for the "inclusive" pion sameples. Thses pions were reconstructed by pairing up photons

one by one while allowing for one photon being paired up with multiple others within the same event. Therefore there is no isolation requirement on the recontructed

pions. Both the yield and background level were increased by a lot. e.g.

 

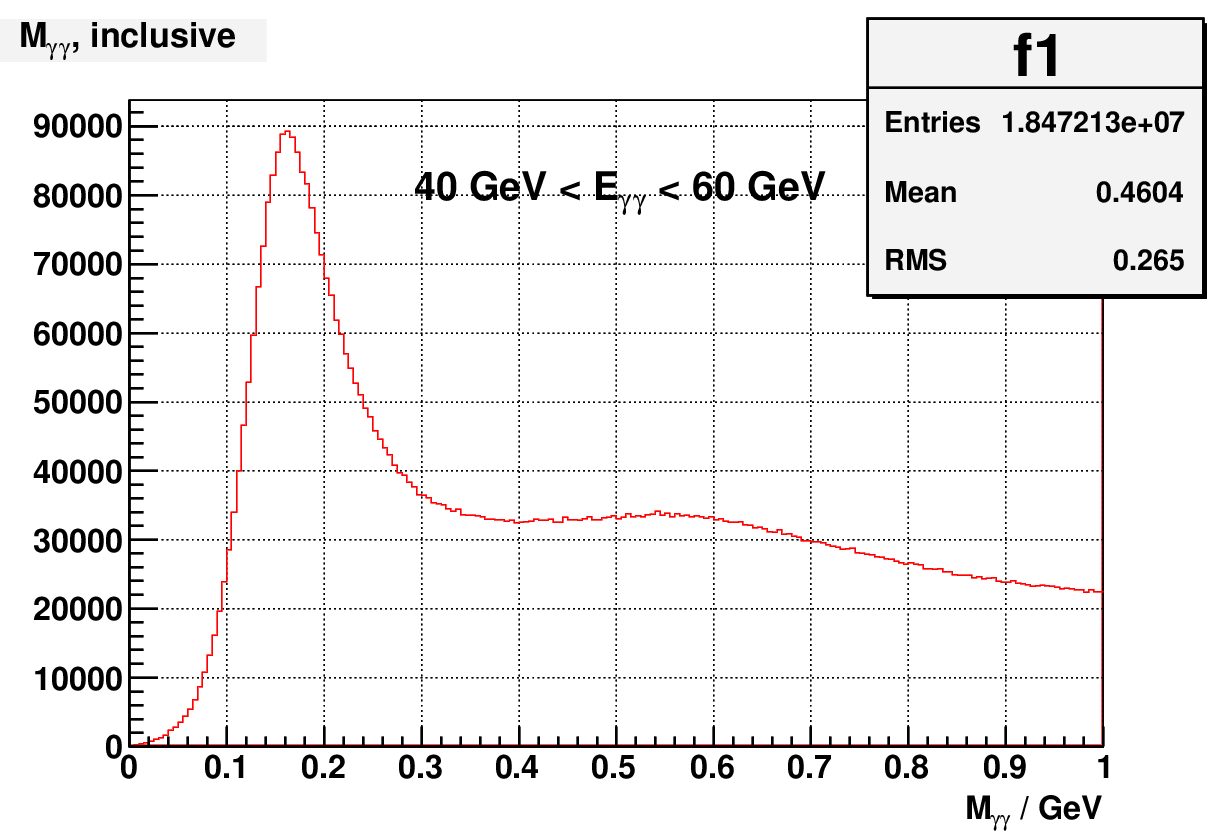
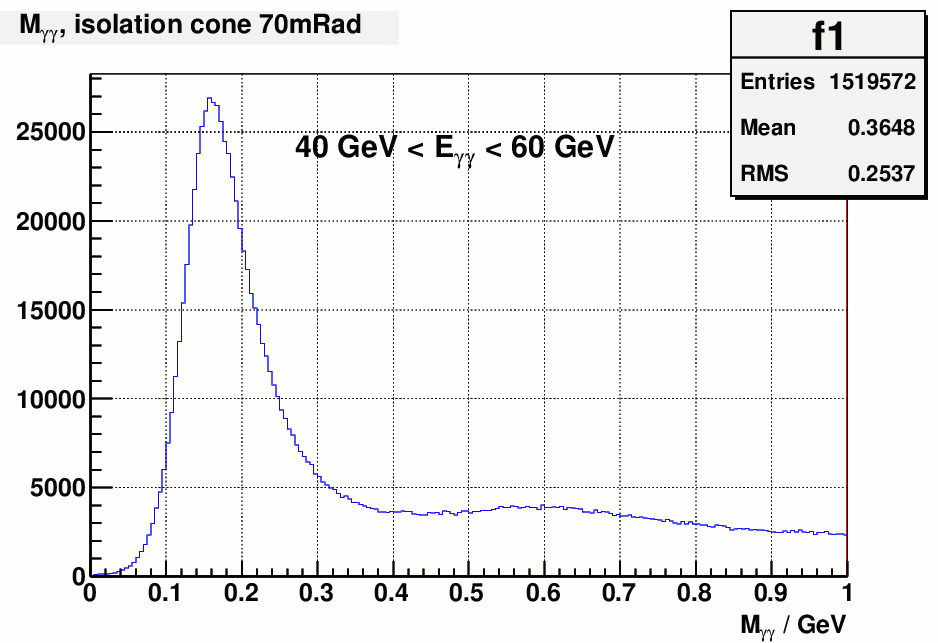
                                                                             fig. 8 two photon masses from Fill_15419

It's interesting to see what the asymmetries of the inclusive pions look like. But subtracting out the background for this sample seems to be necessary.

 

The first thing I trid was random event mixing. Namely each photon from a specific event was paired up with all the photons from multiple other events. The

purpose is to remove the correlation between photons that come from the same pion/eta. However there is also a strong assumption made in order for this

approach to work, that is that photons come from different parents are completely uncorrelated. As we can see below, this assumption is compromised when

there is jet activity present.

  

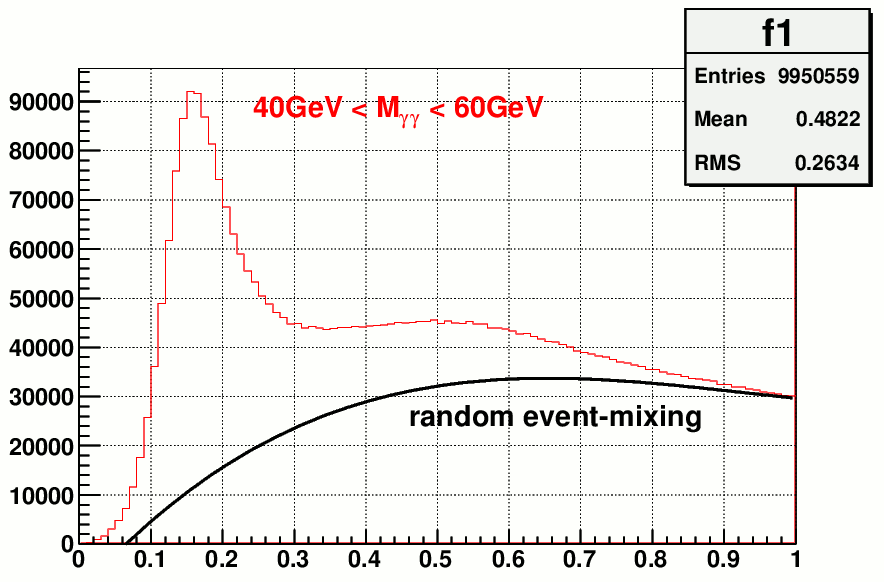
              fig 9 a) inclusive diphoton mass with random mix event bkg                  fig. 9 b) opening angle distribution for data, pion signal from pythia and mix event

 

From fig. 9 b) it can be clearly seen that the 2-photon opening angle distribution has a hump at around 0.02 ~ 0.05 rad which can not be described by the

sum of pion signal and mix event distributions. These residual correlations could be induced by jets.

 

So I did the similar thing as the pion analysis in the mid-rapidity, I ran a jet finder for each event and align the jet axes before mixing two events. This approach

could introduce extra unnecessay correlation if there is no jet for some of events. In the mid-rapidity analysis people managed to get around this by combining the

shapes from random event mixing and jet-aligned event mixing, with a pT dependent weighting factor. But for this analysis I haven't been able to find a decent background

shape no matter how I combine the above two type of mixed events

 

     

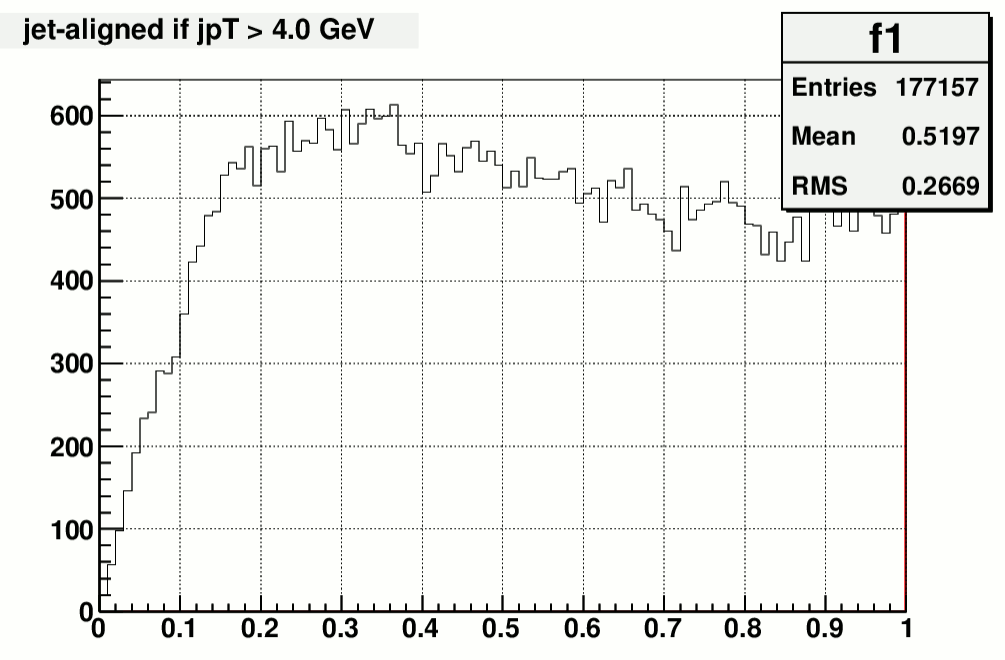
   fig.10 a). diphoton mass frim jet-aligned event mixing, no cut on jet kinematics          fig.10 b) same as a), but only align the jet axes if jet pT > 4.0 GeV

 

          

                                        fig. 11 a)                                                                                                                    fig. 11 b)

From fig.11 a) one can see that there is excessive correlation induced by blindly aligning the jet axes, even for those events that was not

likey to contain a jet.

So I need to figure out a way to suppress these unneceaasay correlations.