Accroding to previous studies, log energy weighted moments + finite energy cut off were able to provide a more distinctive feature to separate 2-photon vs 1-photon clusters. 

Generally what has been observed is that the resultant cluster moment has less dependence on fluctuations on the tails of the shower and event topology ( i.e. whether the photon

hits the center of the cell or the edge ), therefore we can get sharper distributions as a function of cluster energy compared to the traditional energy weighted moments. Admittedly,

the goodness of shower fit is a more advanced tool to separate 1 vs 2-photon clusters, but it also delicately relies on our knowlege of the shower shapes and especially the variance

of the shower shape at difference physical locations ( in order to define a sensible chi2 variable) 

Here I am trying to summerize my understanding of the pros and cons of having lnE weighted cluster moments for pi/r separation, and possible directions to go beyond the current

weighting scheme.

It all starts from a simple principle --to have an indicative variable that will take on different values for different species of the cluster. For example Chi2/Ndf is one possible

way to map the shape information to a single variable and can be used to discriminate 1 vs 2-photon clusters, if defined properly. The next best but relatively quick way is just to look at

the width of the cluster shape. But the defintion of "width" could vary wildy. The simplest one is to use the variance of the cluster shape to represent its width, in some sense this is also

the variance of the number distribution of Cherenkov photons as a function of relative position (or the E weighted 2nd moments), therefore one would have:

                                                e.q 1)

So for a specific cluster, the energy and location of the towers will form a sample which can be used to estimate the variance the parent distribution. But the most important thing to notice

is that the sample variance is representive of the true variance only when the true variance exists. Unfortunately based on our understanding of the shower shape function, its variance

is divergent. One consquence of having divergent variance is that the sample variance could be arbitrary depending on where we put our cutoff. And beyond that the sample variance will also

depend on the shower topology as mentioned above since we only sample a set of discrete points. For a certain cutoff, the calculated variance will be different depending on how far the sampled

points are from the cutoff. Therefore one would have a different cluster moments for showers at the center of a cell vs on the edge. 

                                             figure 1 a).                                                                                                       figure 1 b).

But one good thing about the above plain variance (or energy weighted 2nd moment）is that in princlple it does not depend on cluster energy, provided that the shower shape itself is energy

indepedent. So for a fixed energy cutoff and shower topology, the calculated variance is constant. However this scheme was abandoned because in practice the variations introduced by different

shower topologies is dominant.

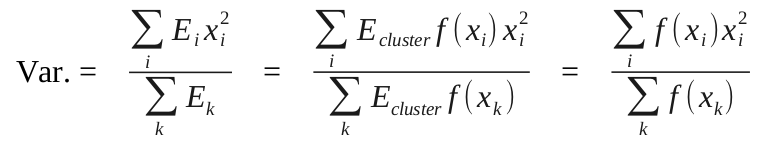                                                    e.q. 2)

Then we moved over to log energy weighted variance. This scheme basically translate the regular shower shape to a new one shown below, then calculate the variance of the new distribution.

Comparing the translated shower shape with the original version one would notice several potential advantages. Firstly a cutoff is naturally introduced by the positivity requirement. Also the shoulder/tail

region acquires more weight than E -weighting and the slope becomes gentler, whereas the top area becomes more flat. All these makes the calculated variance less dependent on where we

sample the shape.

                                                          figure 2                                                                                                 figure 3

But one of the possible drawbacks of lnE weighted variance is that the weigting factor actually depends on cluster energy, as shown in the calculation below (assuming 0.5GeV energy cutoff):

e.q. 3)

in figure 2 I plotted the weighting factor in the numerator as a function of distance. Clearly this facor depends on the cluster energy. For example, figure 2 is the weights for 40GeV clusters. Figure 3

on the right panel is for 120GeV. It can be seen that the lnE weighted cluster moments (or the variance of the translated shape) becomes greater for higher energies even if the original shower shape

itself is energy independent. Additionally, having a cutoff in terms of absolute energy scale(0.5GeV) also makes the weighting factors depend on cluster energy. The trend is verfied by single photon

simulations, as shown below.

                                                  figure 4 a).                                                                                                                               figure 4 b).

There is also a visible hint of increasing sigmaMax as a function of energy in data, as shown in my previous post.

In figure 5 below, I plotted the normalized weighting factors for different energies, as a function of the energy fraction.

So in order to have a weighting scheme independent of cluster energy therefore to provide the real "width" of a single photon or 2 -photon clusters. We need

to remove the energy dependence of the weighting factors. For example by scaling all the lnE factors to the same energy, use

instead of ln E_i