Purity correction for non-identical particle correlations in spherical harmonics

Below I describe the way that the purity correction is applied to the correlation functions expressed in spherical harmonics. This procedure is used when dealing with non-identical particle correlations, where the functions are constructed directly in spherical harmonics (with no intermediate 3D histograms in qout-qside-qlong or q-phi-theta space).

Correlation function in spherical harmonics

The correlation function binned in spherical harmonics is represented as a series of 1D histograms with |q| (magnitude) on the axis. Each histogram corresponds to different l,m component. There are also covariance matrices - these are 2d matices for each q bin, having the number of rows and columns equal to the number of l,m combinations used. We truncate the l,m decomposition of the correlation function at l=3, but practically ony the l=0,m=0 and real part of l=1,m=1 components carry usefull femtoscopic information, while imaginary part of l=1,m=1 is usefull as a diagnostic tool. Nevertheless in the purity correction procedure we use all components up to l=3.

It is important to note that the input to the purity correction procedure is the correlation function which is already properly normalized and has all the background non-femtoscopic correlations removed.

Purity in spherical harmonics

The purity function can also be stored directly in spherical hamonics. We construct such function, by storing in the numerator the pair dEdx PID purity (obtained from MuDst), multiplied by primary particle fractions in a spherical harmonics function, while in the denominator we store unity for each pair. Then eploying the standard formalism to compute the correlation function directly in spherical harmonics, we obtain the purity function, also represented directly in spherical harmonics.

Standard purity correction

Applying a purity correction is a fairly straightforward procedure which is well established in femtoscopy. It is written as:

C_corrected(vec q) = (C_measured(vec q) - 1)/P(vec q) + 1

It is usefull to define the correlation effect R as:

R(vec q) = C(vec q) -1

and then the purity correction procedure simplifies to:

R_corrected(vec q) = R_measured(vec q)/P(vec q)

Purity correction with functions in spherical harmonics

In spherical harmonics decomposition, to obtain R from C one simly has to subtract 1.0 from the C00 histogram and leave all the others unchanged. Which means that applying the purity correction is actually quite simple: one uses the standard formalism to calculate the correlation function directly in spherical harmonics, treating R_measured as the numerator and P as denominator. The result is R_corrected. To come back to C_corrected, one simply has to add unity to the R00 histogram and leave all the others unchanged.

The resulting C_corrected is the final experimental result, which can then be an input to the fitting procedure and quantitative analysis.

Example correlation function

Below I show an example of how the correlation function is changed with the purity correction.

First a correlation function (pi⁺K⁺), properly normalized and with the non-femtoscopic correlations removed:

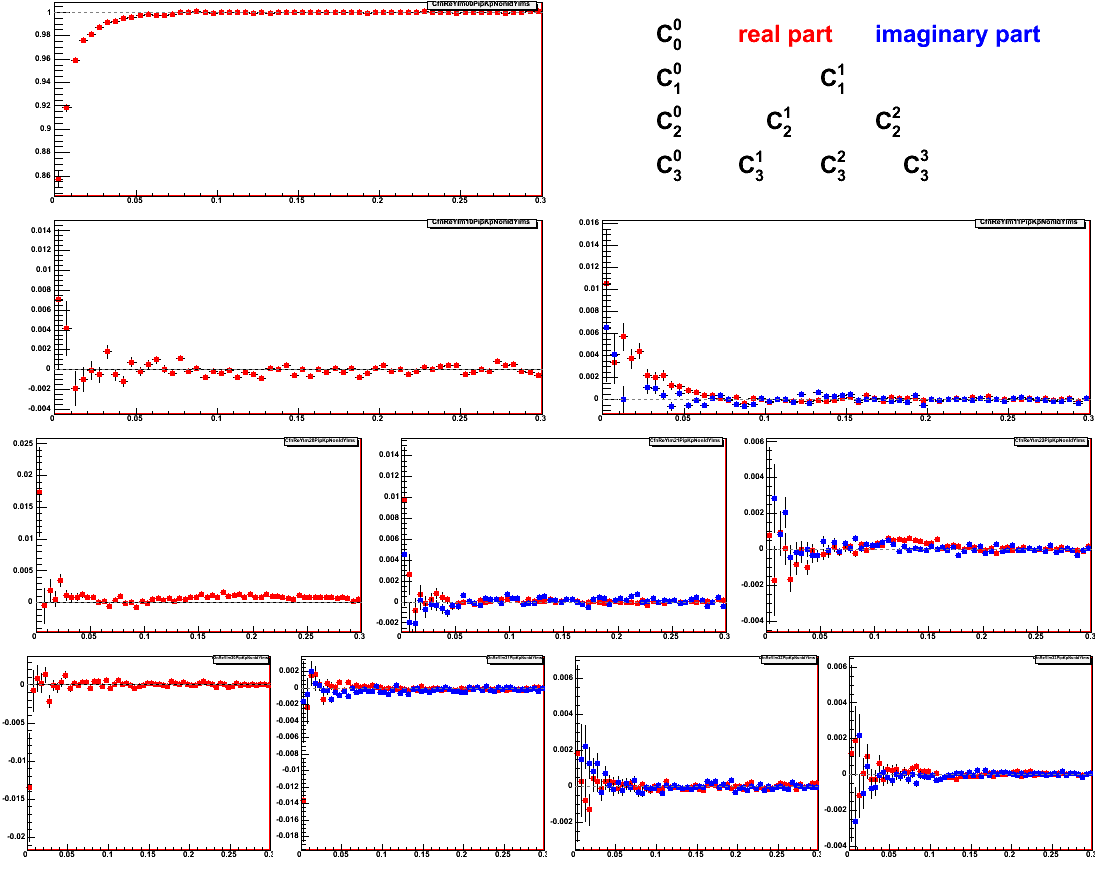
Please note the scale on the y axis in C00 and C11.

Then the purity correlation function - based on the PID purity probability obtained from data:

One can see that average pair purity is on the order of 0.7. What is also important is that the purity function has some structure both as a function of k*, as well as directional dependence. All this structure is automatically taken into account in the purity correction procedure, which uses all l,m components.

Finally the corrected correlation function:

As expected the correction does not change the general behavior of the function. The correlation however is increased, please compare the scale on the y axis in C00 and C11 in the above plot and in the uncorrected plot. The purity correction procedure works as expected, while utilizing the full available information on particle purity as a function of relative momentum magnitude and direction.