Non-identical particle correlation functions - normalization

When calculating the correlation function for non-identical particles we have identified several physics and non-physics related effects that influence the function. It was found that the spherical harmonics decomposition is especially usefull in analyzing the function, since it compresses the full 3D information into a few 1D plots. The others vanish due to symmetries. Below is the list of the effects in the correlation function, together with their expected effect on various spherical harmonics moments:

1. The correlation effect itself. - it is expected to be mainly visible in C00, as a difference from unity. Same-sign pairs will show a drop at low k*, opposite-sign pairs will show an increase.  The magnitude of the drop/increase should be proportional to the source size. The asymmetry signal is expected to be present in real part of C11, as a deviation from zero. In principle it can go both below and above unity, however the flow scenario clearly predicts which way it should go. For same-sign it should go above unity, for opposite-sign - below untity. Such an effect is consistent with the scenario where pions/pions/kaons are emitted on average closer to the center and/or later than kaons/protons/protons for pion-kaon, pion-proton and kaon-proton pairs respectively. The above mentioned picture has one exception - opposite-sign kaon-proton pairs, where the strong interaction is significant and overwhelms the Coulomb effect at certain range of k*, making the correlation function go below unity (which should flip the sign of Real C11 as well). Some effect is also expected in the real parts of C20 and C22. As shown by pion correlation these components deviate from unity if out, side and long source sizes are different. It is however unclear if our data has enough sensitivity to see this. Also note that changing the magnetic field orientation should NOT change the behavior of C00 and C11.
2. Event-wide correlations - apart from the femtoscopic correlations there are other, event-wide correlations which will be reflected in Cxx. These include elliptic flow, minijet-type correlations, energy and momentum conservation etc. Following the studies done for dAu systems one should expect these to show in C00 and real part of C11. They might also show in higher order components (e.g. l=2). The should not influence imaginary parts of Cxx. They should also not change when You change the magnetic field orientation, since these are genuine physical correlations and not a detecor/reconstruction effects.
3. Hit sharing/track merging - this is a known detector effect present in all correlation functions. We use a specific cut ("Hit-merging cut") to remove it. However some residual effect remains. The effect means that in the numerator there is a depletion (with respect to the denominator) of pairs at a certain angle phi (in the transverse plane). This will surely influence the Imaginary part of C11. It will also affect C00. It may indirectly affect real part of C11, through the effect it has on C00. This is detector effect and thereore it has some peculiar properties: it should switch sign in Im(C11) as we change particle signs (e.g. the effect for pi+K- should have opposite sign than the effect for pi-K+), but the effect on C00 should stay the same. The sign flip should also happen when we chenge field polarity. Taken all the above into account the effect should be easily identifiable.
4. Electron-positron pairs - correlated electron-positron pairs coming from gamma decays, misidentified as geuine non-id pairs (pion-kaon, pion-proton, kaon-proton) are another major detector problem. We are using a highly sopisitcated anti-gamma cut to reject them, but again a residual number of them remain. They should have similar effect on the C components as the hit-merging effect, with the following differences: only opposite-sign pairs are affected. The effect is at lower k*, just due to the kinematics of the problem.

With the above considerations one is confronted with a following problem. One has the measured components of C00, Re(C11) and Im(C11) (and higher-l components if needed). One has to identify and quantify all the above effects and than extract from these only the relevant part of the information. That means we want to identify and isolate deviations in C00 Re(C11) and Im(C11) due to the effects 2., 3. and 4., and treat them as "background" in order to extract a properly nomalized C00 and Re(C11) which will contain only effects due to 1.

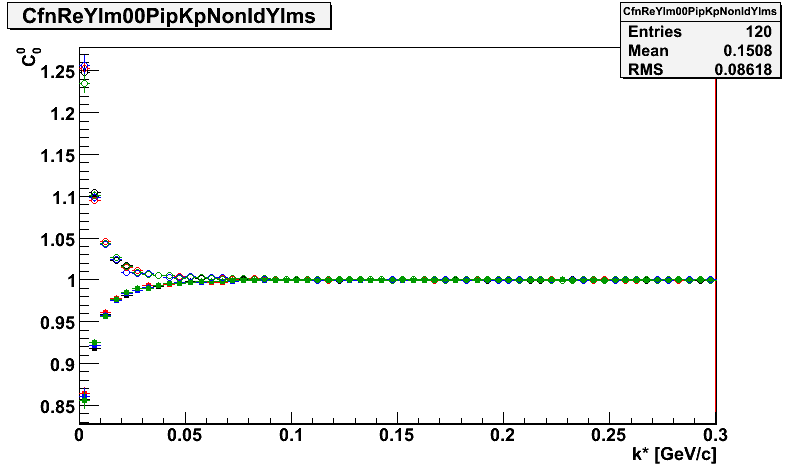
First let's look at the example plot to see if the function behaves as expected.

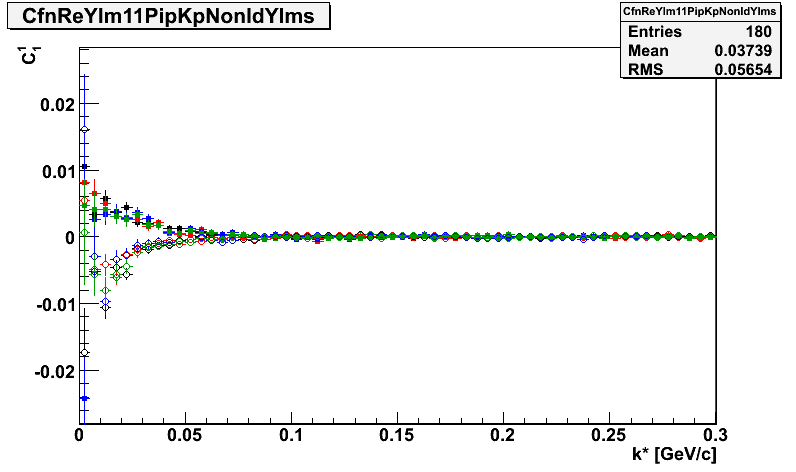
Please note that the scale on y axis on all the plots is the same for comparison. The points are same-sign pion-kaon correlations: black - pi⁺K⁺ Reversed full field, red - pi^-K^- Reversed Full Field, green - pi⁺K⁺ Full Field, blue - pi^-K^- FullField. Let's analyze the plots with respect to the effects described above:

1. The correlation effect is there - points go significantly below unity at low k*. This is good as the expected femtoscopic effect is much larger than any background. In Re(C11) we also see a large and consistent deviation at low k*. However there seems to be an additional effect in Re(C11)

2.Apart from the expected femtoscopic bump at low k* there is a large scale "baseline" in Re(C11) it seems to be practically linear in k*, it follows the expectations for the event-wide correlation. In order to "remove" it one has to assume some functional form with which to extrapolate the trend to the lowest k*. A first or second order polynomial seems to be reasonable. One should also note that the downwand slope in Re(C11) seems to be mirrored by the upward slope in C00.

3.One sees a strong effect consistent with "hit-merging" in Im(C11). It has exhibits the expected sign flips and sits in the k* range consistent with the simulations of the effect.  One should also note that the "bump" at 0.1 GeV/c in Im(C11) corresponds to the "bump" in C00, where the function goes above unity (which is not expected from the Coulomb dominated CF). The share of Im(C11) seems to be a bit complicated, one can assume that a 5-th order polynomial may be able to fit it.

4. gamma pairs seem to be absent, which is expected for same-sign pairs.

Taking the above observations into account, one can proceed with the deteminator of a "backgound" and then its removal and subsequent "normalization" of the femtoscopic effect only.

First let's concentrate on Im(C11) as it clearly shows detector effects and should not contain any "femtoscopic" component. Therefore one can try to fit it with

B_I11 = f *(a_S + b_S * k* + c_S * k*² + d_S * k*³ + e_S * k*⁴ + f_S * k*⁵)

Please note that we use a single set of parameters for ALL FOUR Im(C11) only changing the factor f as the effect is expected to flip sign: 1.0 for pi⁺k⁺ RF and pi^-K^- FF and -1.0 for pi^-K^- RF and pi⁺K⁺ FF. We will use the final fitted form of B_I11 when dealing with C00 later.

Then let's look at Re(C11) there is a femtoscopic effect at low q, which can be approximated by e.g. a gaussian, and a non-femtoscopic background approximated with a polynomial. So we proceed to fit Re(C11) with:

M_R11 = B_R11 + F_R11

F_R11 = l*exp(-k*² R²)

B_R11 = a_R + b_R * k* + c_R * k*²

Again we perform this fit to all four Re(C11)'s a the same time. We separate the measured function M_R11 into the "background" part B_R11 and the "femtoscopic" part F_R11.

Finally, with the background parameterizations at hand, one can look at the C00 - the correlation function itself. We expect to see the combination of all components in here: the femtoscopic effect, event-wide correlations and contaminations. We try to fit the C00 with the following function:

M_C00 = N*(1 + p/(R_f a_c k*^1.75)) + m*B_R11 + m*B_I11

Where N is the overall normalization, B_R11 and B_I11 are the background terms, which were fixed in the previous steps, m is a multiplier by which we scale the background factors (it is a free parameter). The last term is the approximation of the femtoscopic effect and deserves a detailed explanation.

a_c is the Bohr radius of tha pair, characterizing the Coulomb interaction. R_f is a parameter which is connected to the size of the system. p is the average pair purity for a given pair. Now we discuss the particular form of this component:

It is known that a Coulomb interaction, at sufficiently large momentum difference k* and/or space-time separation r* can be approximated by the form Psi = 1-1/(r* a_c k*²). This is however valid only for a single pair. A correlation function is an average pair weight: C = <Psi>, where the averaging is done at fixed k* for all r*. Out of the pairs which will be used in the averaging only some will be in the region of the validity of the asymptotic form. For the rest one has to calculate the full pair wave function. Therefore, the exact asymptotic funtional form of C can only be obtained from numerical calculations. Such calculations were performed, and it was empirically found that the form 1+1/(R_f a_c k*^1.75) fits the asymptotic behavior best. It is a reasonable functional form, which is close, but not identical to, the asymptotic form of the wave function for a single pair. This form however can only be used with some caveats: It is valid for "sufficiently large k*", which were empirically found to be above 100 MeV for pion-kaon and pion-proton pairs and 150 MeV for kaon-proton. It must be scaled down by the "purity" factor p if we are fitting the "raw" correlation function (which is the case here). The R_f parameter is certainly related to the source size, however no formal definition or relation to the proper gaussian source size R_G is known.

So in the end the following parameters are free in the fit to the correlation function:

• Normalization N
• backgroung scaling m (which is expected to be close to 1.0)
• asymptotic size R_f

All the others are fixed, either by fits to other components (B_R11 , B_I11), from data (purity p) or are constants (a_c).

After the fit is done, we proceed to produced the extract the "femtoscopic signal" from our correlation funcion, that is to calculate:

F_C00 = (M_C00 - m * B_R11 - m * B_I11)/N

F_C11 = M_C11 - B_R11

Only after this procedure the purity correction can be applied to the correlation function.

Below is the example of the fit, for the opposite charge combinations of pion-kaon pairs:

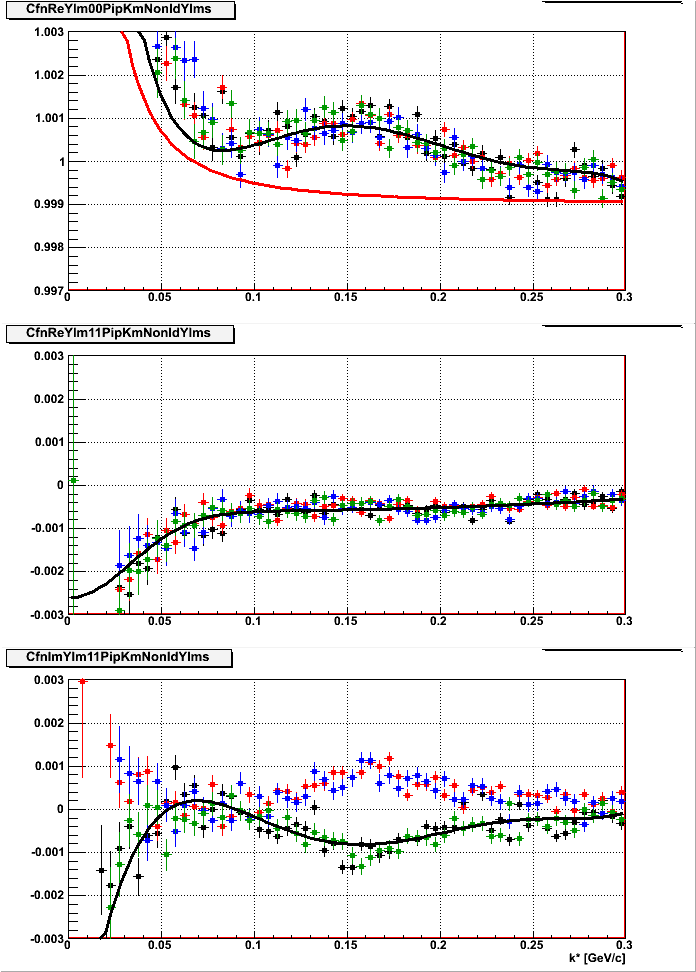
The middle plot show Real parts of C11 for all pair combinations. Color coding is as follows: black- pi⁺K^- Reversed FullField, red: pi^-K⁺ Reversed Full Field, blue - pi⁺K^- Full Field, green pi^-K⁺ FullField. the black line is the fit of B_R11 + F_R11 to all the functions at the same time.

On the lower plot, the Imaginarty parts of C11 are show, the black line is the fit of B_I11 to all of them at the same time.

The upper plot shows C00 for all pairs. Again, please note the large zoom on the y-axis, the actual correlation effect goes to about 1.25 for the lowest k* bin. The black line shows the full fit of the C00, together with all the backgounds in. The red line shows the "femtoscopic effect" only, multiplied by the normalization. In other words the difference between the black and red line is the influence of the background.

Clearly the influence of the background is rather strong at large k*, however in our fits we restrict ourselves to the region below 0.1 GeV/c in k*. The normalization and background removal procedure will be a source of a systematic error. One can try different functional forms of parameterizations of BR11 and B_I11 to see what effect it will have on the final fit radii. One can also try to fit normalize each pair separately and see what is the difference to the case when the backgrounds are determined in a combined fit.

Finally I show the raw correlation functions properly normalized and with background removed according to the above procedure. Next step in the preparation of these functions is the application of the purity correction.