Towards understanding contributions to the h^-/h⁺ issue seen in global tracks, Maxim & I discussed finding out how well we need to calibration the alignment parameters. I've thrown around numbers before, but it's important to have something definitive.

To get an answer, I ran 5 jobs on 250 events, yielding ~250k global tracks which pass some quality cuts (these are the same cuts used in selecting tracks for SpaceCharge+GridLeak calibrations):

1. At least 25 TPC hits
   1. At least 5 hits in the inner sector
   2. At least 10 hits in the outer sector (redundant with 25 total hits)
2. 0.3 < p_T < 2.0 GeV/c
3. |η| < 1.0
4. Both 2D and 3D signed DCA from primary vertex < 4 cm, where the vertex satisfies:
   1. Rank (VFMinut) > -5, and is highest rank in the event
   2. At least 5 daughter tracks
   3. At least one daughter matched to EMC
   4. |V_Z| < 50 cm
5. No TPC hits on the track from beyond the central membrane (signature of post-crossing tracks, PCTs)

The 5 jobs were as follows:

1. Run 10 alignment parameters
2. Same as (a) but with innerSectorRotationAngle shifted by +0.02 degrees
3. Same as (a) but with innerSectorRotationAngle shifted by -0.02 degrees
4. Same as (a) but with outerSectorLocalxShift shifted by +0.02 cm (+200 μm)
5. Same as (a) but with outerSectorLocalxShift shifted by -0.02 cm (-200 μm)

I then matched up tracks between the different jobs and placed various quantities from them into an ntuple, allowing me to view dependencies and correlations (I have attached a tarball of the code I used). In particular, I studied the changes to pT of global tracks, as well as changes to their signed DCA, which will translate into two issues: (1) topological reconstruction of secondary vertices, and (2) primary track momentum reconstruction. The various figures on this page generally show 4 panels:

• top first column: derivative with respect to the innerRotationAngle
• bottom first column: second derivative with respect to the innerRotationAngle
• top second column: derivative with respect to the outerSectorLocalxShift
• bottom second column: second derivative with respect to the outerSectorLocalxShift

The exception will be the first figure, where two more panels will appear in a third column on the right, to be explained momentarily. I will place some discussion above each plot.

In the plots, the vertical extent of the red bars represents the error on the mean, while the black bars indicate the distribution RMS. The former is representative of the statistics I used, while the latter is representative of the reconstruction resolution (how moving hits around within their errors affects the ability to reconstruct the same quantity).

________________________________

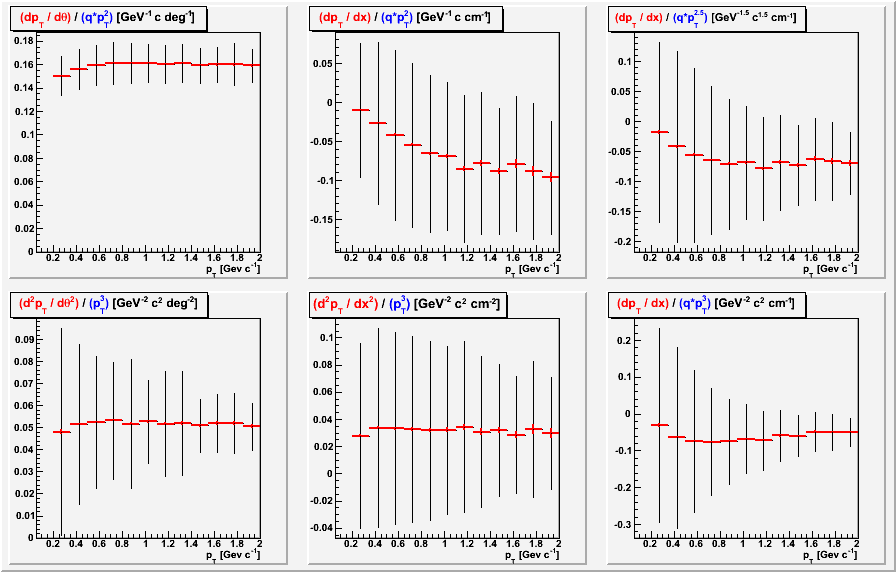
d(p_T) vs. p_T

This is perhaps one of the most relevant plots for h^-/h⁺. From investigating that issue, we believe that the problem is at the level of δ(p_T) ~ 0.002 * q * p_T². Here, we see that per degree of shift in the innerSectorRotationAngle, we introduce δ(p_T) ~ 0.16 * q * p_T², and per centimeter of shift in the outerSectorLocalxShift, we introduce δ(p_T) ~ -0.10 * q * p_T² (at least it appears to be approaching this at high p_T). This means that the h^-/h⁺ problem can be due to an incorrect innerSectorRotationAngle of (0.002/0.16) * 1 degree = 0.0125 degrees, or an incorrect outerSectorLocalxShift of (0.002/0.10) * 1 cm = 200 μm. The stipulation is that the calibration of these two quantities must be better than these scales!

The right column of panels attempts to see if the dependence in the derivative is perhaps more like p_T^2.5 or p_T³, but the cube is certainly too much, and it may be that the 2.5 power is also too much at higher p_T. We expect the dependence to go with q * p_T²  because spatial distortions correspond to track curvature (1/p_T) shifts, so a constant value of δ(1/p_T) = C approximates to δ(p_T) ~ C * p_T², or δ(p_T)/p_T ~ C * p_T (with some additional effects of multiple scattering at low p_T). It just appears that the approximation of being at high enough p_T to ignore additional effects goes to a slightly higher p_T for the outerSectorLocalxShift.

The second derivatives appear to be generally flat with p_T when scaled by p_T³. This is probably because if dp_T = p_T² d(1/p_T), then d²p_T = (2p_T³+p_T²) d²(1/p_T), which is dominated by the p_T³ term for p_T above half a GeV/c. Note that the second derivatives are independent of charge sign.

 

________________________________

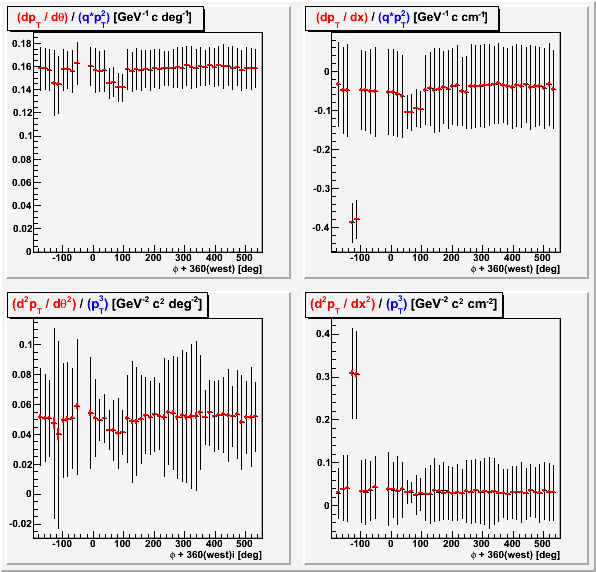
d(p_T) vs. φ

Here we can see the east side sectors on the left and west side sectors on the right (2 bins per sector), where I have made the additional cut that the first and last points on the track are on the same side of the TPC and each is at least 40 cm from the central membrane (to be sure we exclude PCTs).

• Sector 20 has no tracks which pass the initial quality cuts due to dead regions and is blank.
• Sector 17 (near -120 degrees) seems particularly sensitive to the outerSectorLocalxShift.
• Sectors 23 and 24 are also outliers. There were notable dead regions in these two sectors.

For all other plots on this page (including the ones above this), I have excluded these 4 sectors!

 

________________________________

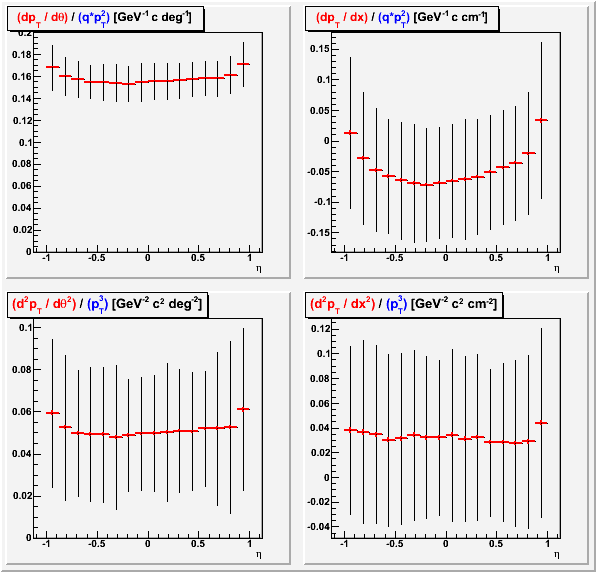
d(p_T) vs. η

These distortions likely change the transverse reconstruction of the track hits, but not the longitudinal. That will change the track dip angles, and therefore the pseudorapidity. I am not sure offhand why it is asymmetric about zero, but it may have to do with the distribution of tracks within the acceptance due to a non-centered primary vertex distribution?

 

________________________________

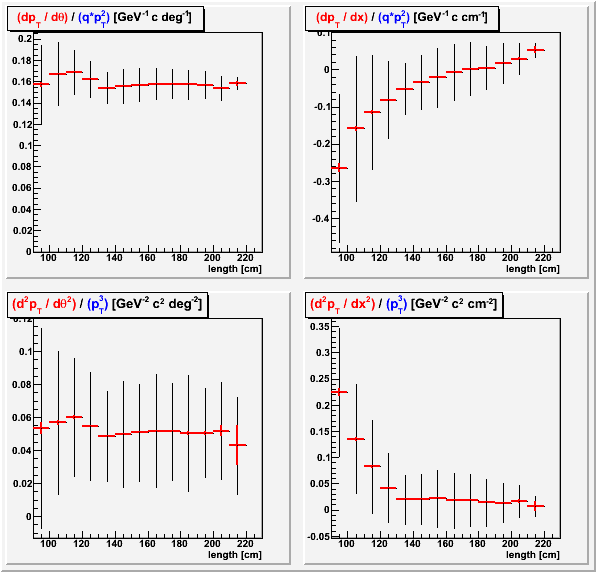
d(p_T) vs. track length

Not much dependence for the angle shifts, except for short tracks. But the offsets shifts show a very strong track length dependence. I haven't fully digested this, but it does say that short tracks are the most affected by offset shifts.

 

________________________________

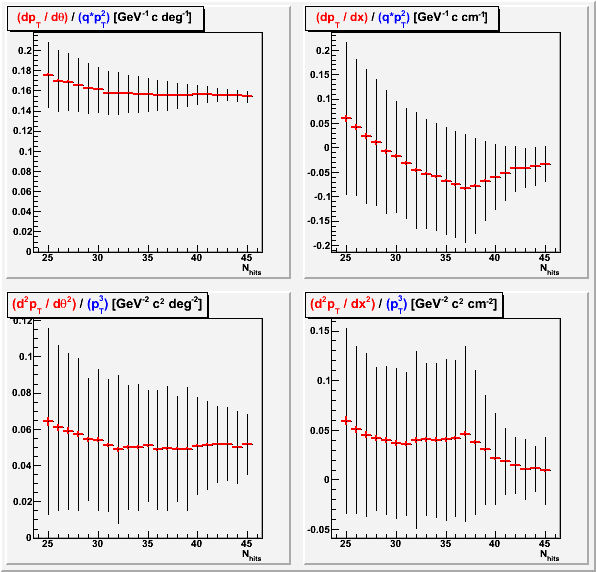
d(p_T) vs. N_hits

This shows a very curious behavior for the offset shift dependence, with a kink at 37 hits. This is 8 less than a perfect 45 hit track, so it may have something to do with missing outer RDO or anode sections from a few TPC sectors. This may also have some correlations with the track length dependence shown previously.

Tracks are required by my initial quality cuts to have at least 25 TPC hits.

 

________________________________

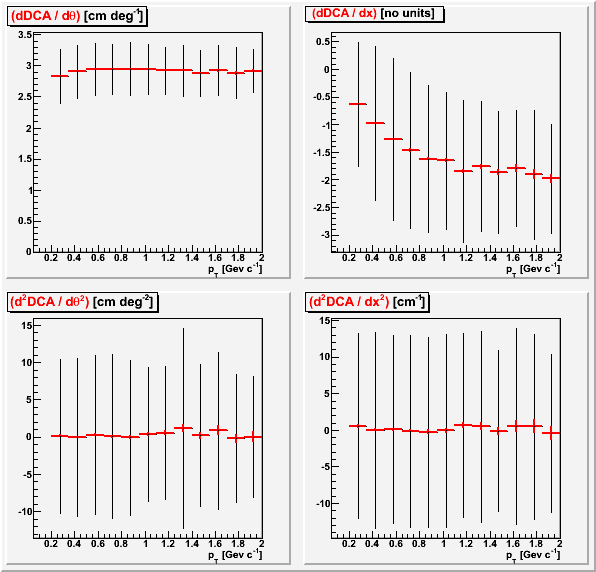
d(DCA) vs. p_T

Since the introduced distortion from changing the alignment parameters is in physical space, it makes sense for a fixed change in the parameters to introduce a fixed change in something physical like the signed DCA. This holds true for the changes to the innerSectorRotationAngle, where the signed DCA changes by 3 cm per degree of rotation without scaling by anything, with no second derivative (note here that despite my cut on signed DCA < 4 cm, I'm actually making a much smaller change and scaling it up).

The change in outerSectorLocalxShift seems to behave a little differently, leading to a smaller effect on low p_T tracks. This is similar to what was seen for d(p_T) / q*p_T² vs. p_T.

 

________________________________

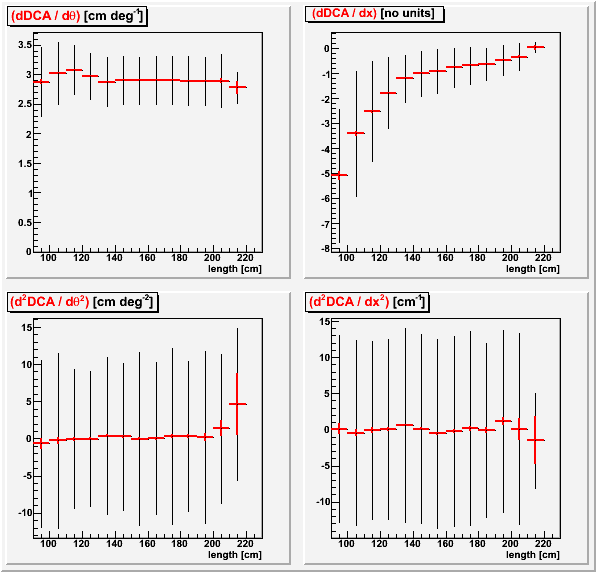
d(DCA) vs. track length

The dependence of d(DCA) with track length is again similar to what was seen with d(p_T) / q*p_T² vs. track length: flat for innerSectorRotationAngle changes except for a small oddity at short track lengths, and significant changes for outerSectorLocalxShift at short track lengths. Again, second derivatives appear to be zero for d(DCA).

 

________________________________

 

-Gene