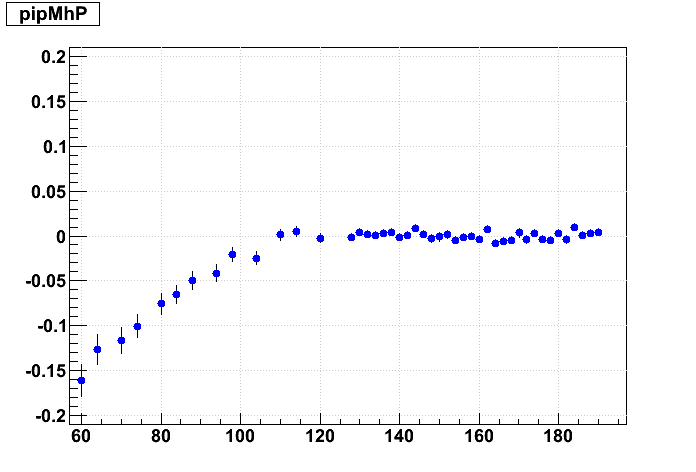
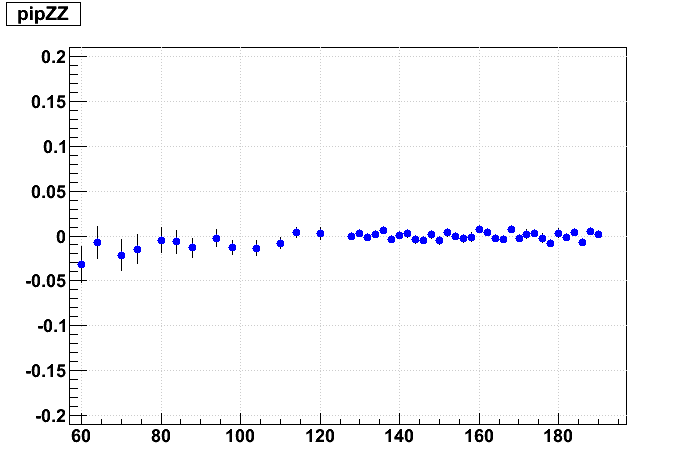
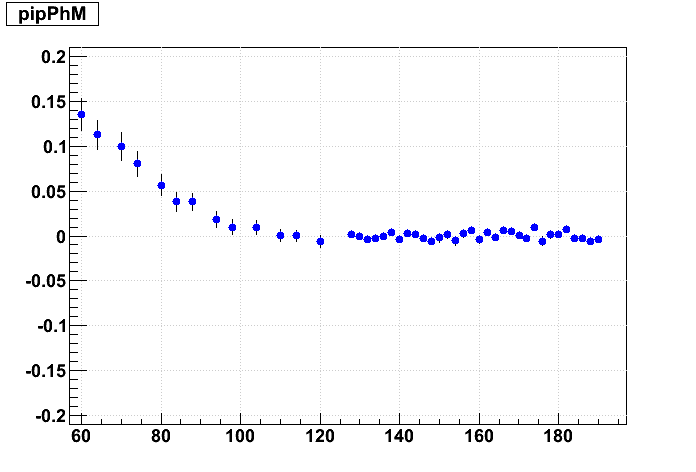
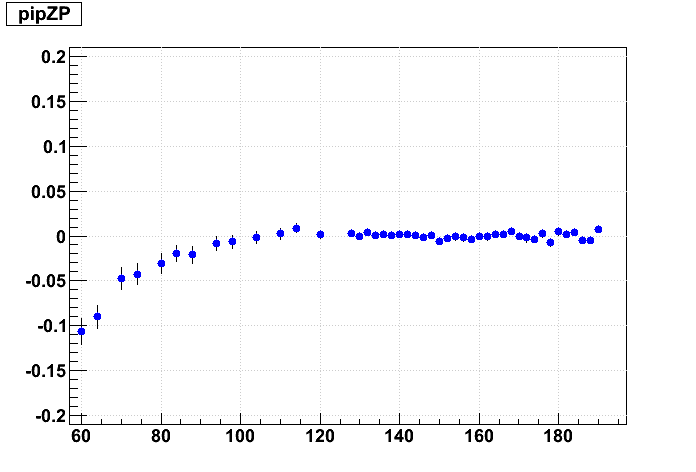
Ths distortions due to sector misalignments depend not just on internal sector alignment (inner-to-outer), but also the supersector alignments. Here this is demonstrated by looking at the residuals on simulated 500 GeV/c pions, leaving inner TPC hit errors very large so as not to constrain the tracks.

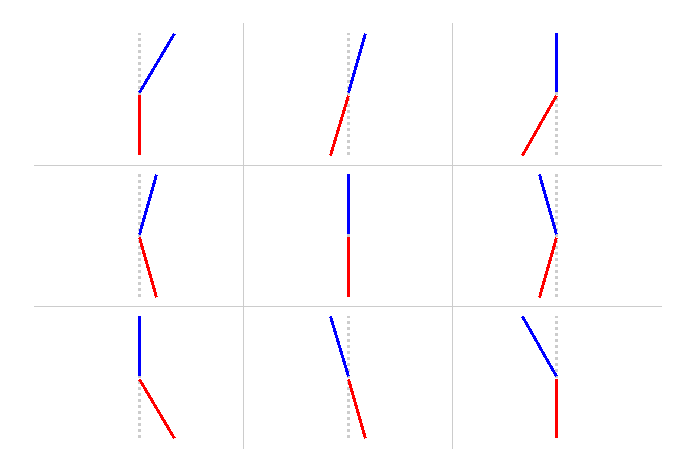
I misalign all inner and outer sectors by a relative angle (internal alignment angle Δα) of 4 mrad in one direction in the left colum, and 4 mrad in the opposite direction in the right column, and no relative angle in the middle column. The super sectors are rotated going from top row to bottom row in 2 mrad steps, keeping the internal angle the same. Here is a graphical representation of the misalignments I've given the outer (blue) and inner (red) sectors (grey dots represent ideal positions):

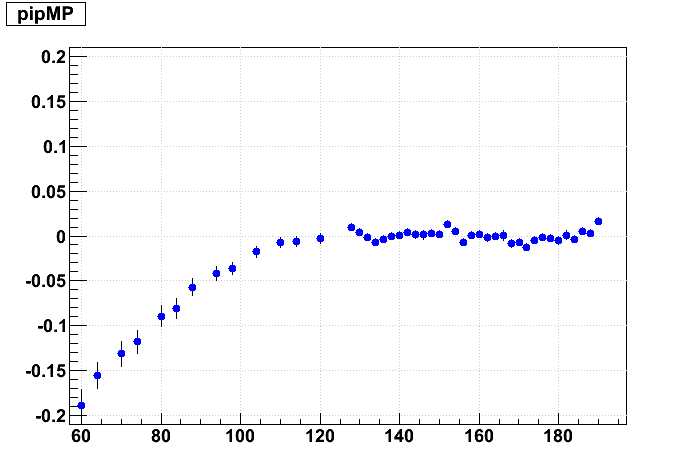
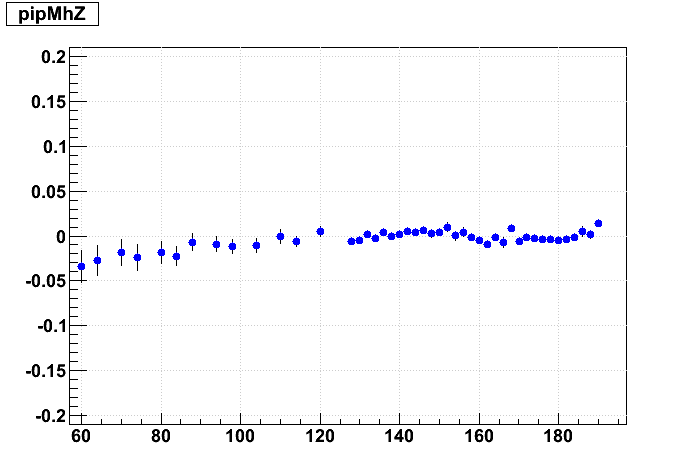
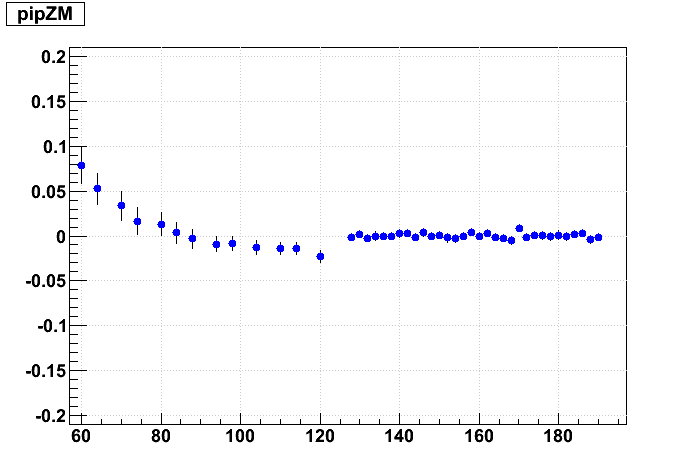
And now the resulting residuals:

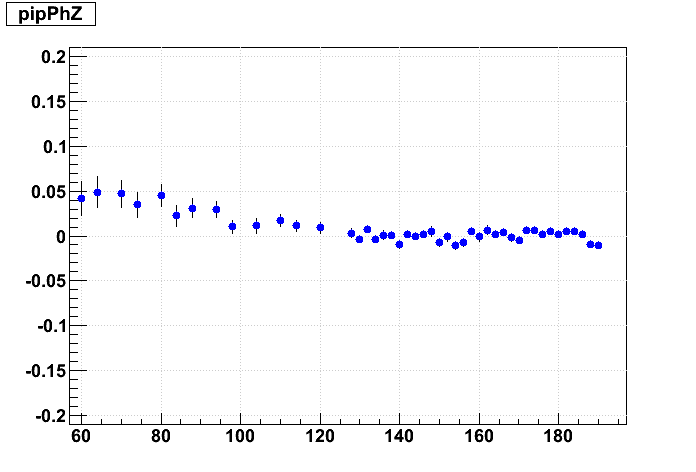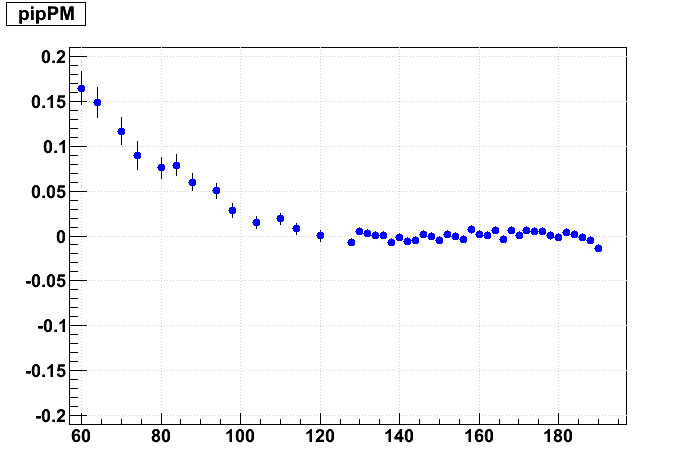The supersector alignment certainly has a visible effect and contributes to the distortion. A 4 mrad change in the supersector Δα alignment angle induces about 1 mm of residual on padrow 1, while 4 mrad of internal sector Δα alignment depends on how one chooses to implement this angle: (i) holding the outer sector fixed and rotating the inner induces about 1.0 mm of residual on padrow 1, (ii) holding the inner sector fixed induces about 2.0 mm of residual on padrow 1, or (iii) moving each by half induces about half the effects, or ~1.5 mm. I believe we implement (ii) in our codes: internal alignment keeps the inner sector fixed, so it is represented by going from upper left to lower right in this matrix, while supersecor alignmnt is represented by going from top to bottom. The effect on the residuals is twice as sensitive to outer sector rotations as to inner.

To put that in alignment context, 1 mm over ~600 mm between padrows 1 and 13 leads to ~1.6 mrad in internal sector Δγ. We are hoping to explain approximately ±0.5 mrad depending on B field sign, but the initial findings on Δα are closer to 0.4 mrad than 4 mrad, so these misalignment distortions may not sufficiently explain the field dependence.

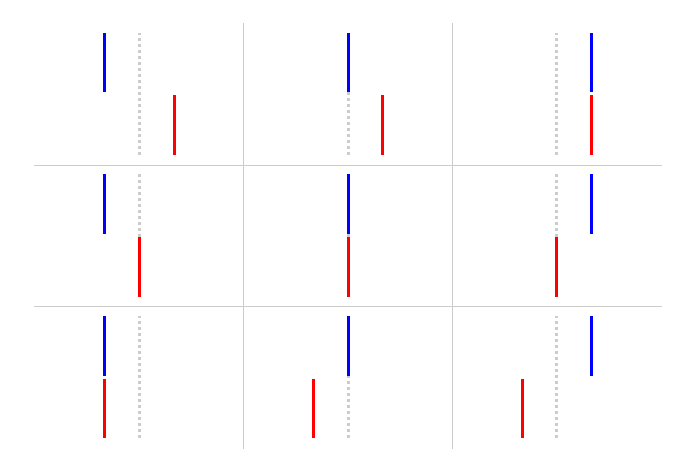
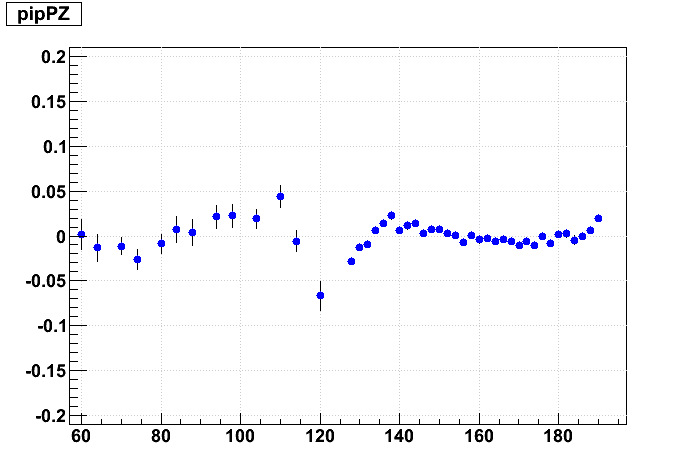
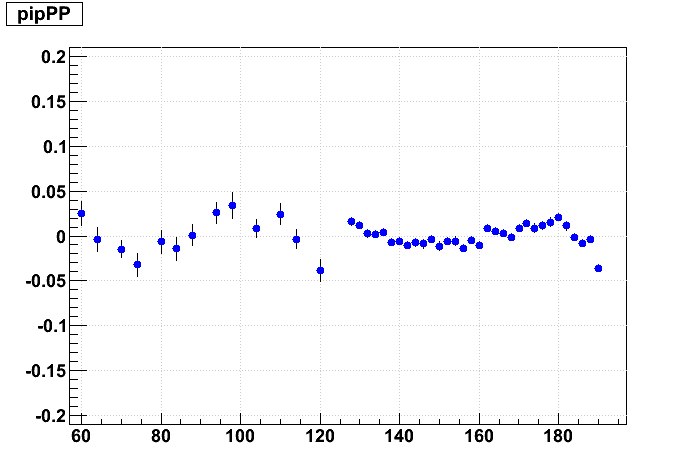
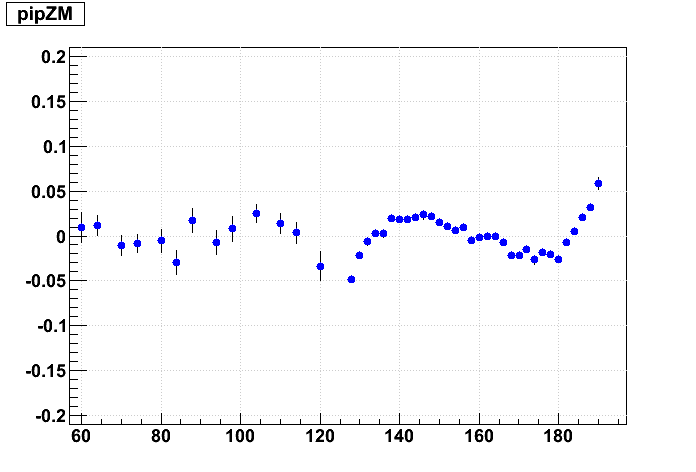
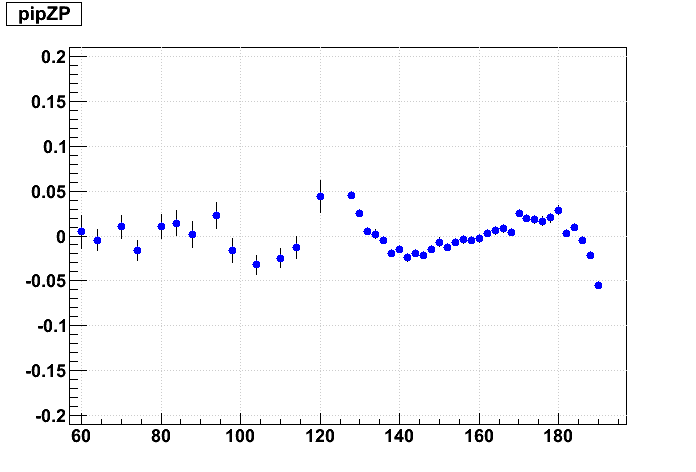
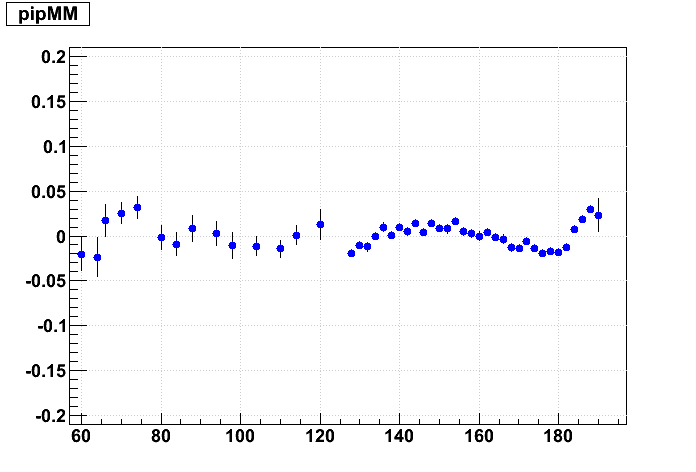
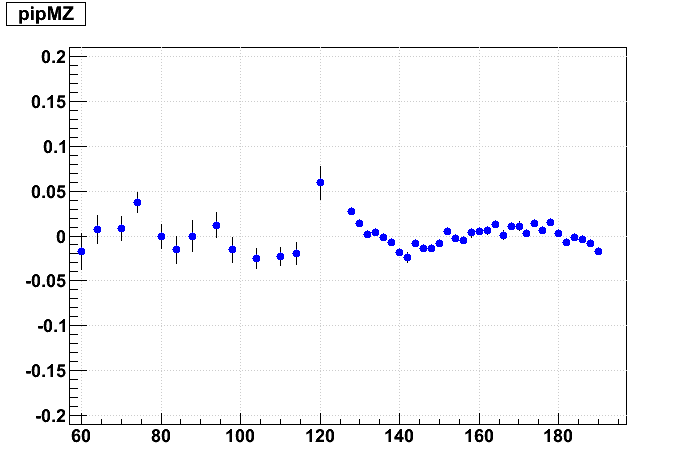
Next is the effect of 1 cm Δz shifts. Here is a graphical representation of the misalignments I've given the outer (blue) and inner (red) sectors (grey dots represent ideal positions):

And now the resulting residuals:

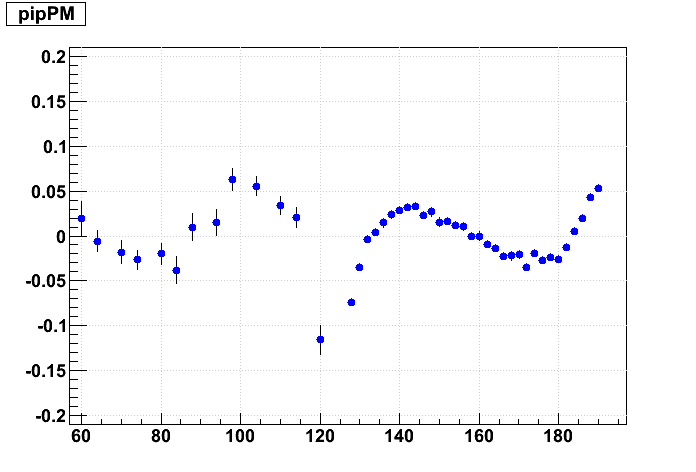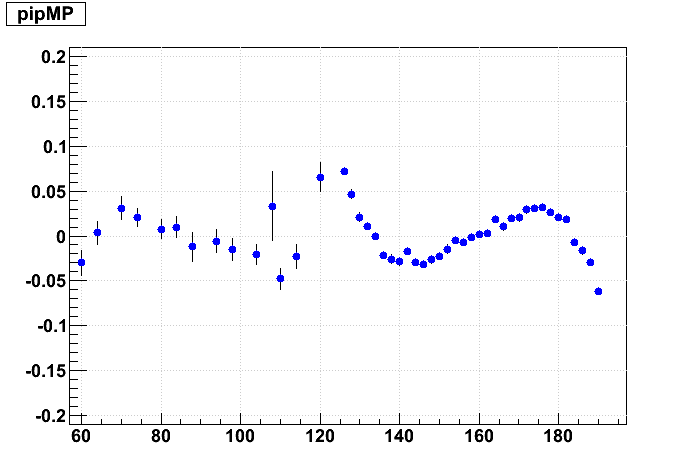These 1 cm shifts are much larger than we should expect to see in the real data. They introduce much more confusing artifacts in the residuals, causing both the inner & outer sector residuals to form "S" shapes. By eye, the effect of these shifts is not very large in terms of a slope and offset for a straight line fit to the inner TPC residuals. And shifting the supersectors has a much smaller impact than internal sector misalignments.

For this matrix of shifts, because we keep the inner sectors fixed in internal alignment, internal alignment is represented going from left to right, while supersector alignment is represented going from lower left to upper right.

I have, so far, still ignored Δβ rotations and effects due to neighboring sectors in this particular study.

-Gene