The TPC SpaceCharge & GridLeak distortions lead to effective rotations of tracks about a radial position somewhere in the middle of the TPC. For example, for SpaceCharge, this point is believed to be at a radius of 97 cm, and any track is essentially rotated about the point at which the track crosses this radius. I'm not sure what the radial position is when GridLeak is also taken into account, but I believe the model holds.

This has long been known to result in a de-focusing of tracks at the primary vertex, which, to first order, should allow vertices to still be found at the correct position when using tracks from all azimuths. A second order effect is already known to exist in tests of the Minuit Vertex Finder, which show a clear bias in vertex reconstruction towards (0,0) when these SpaceCharge & GridLeak distortions are changed (i.e. de-tuned, such that the de-focusing occurs).

While that observed effect is as yet still not fully understood, I have been able qualitatively to demonstrate a perhaps related effect through a model. Interestingly, what I see from my model is an introduction of vertex position biases orthogonal to the direction towards (0,0) [tangentially?]...

When tracks get their distortion rotation, there is no consideration in the distortion for the origin of the tracks. This means that tracks are de-focused equally in their pointing towards (0,0), but not necessarily equally in their pointing towards the primary vertex position (V_x,V_y), especially when the primary vertex is not at (0,0). The closer the primary vertex is to the track's rotation center, the less impact the rotation has (in the extreme, if the primary vertex were at the radius of track distortion rotation at some particular azimuth, tracks at that azimuth would still go through the primary vertex after distortion, but tracks from the opposite side of the TPC would miss the primary vertex greatly). However, because the radius about which tracks are rotated is much larger than the distance by which the primary vertex is offset from (0,0), this is not a first order effect.

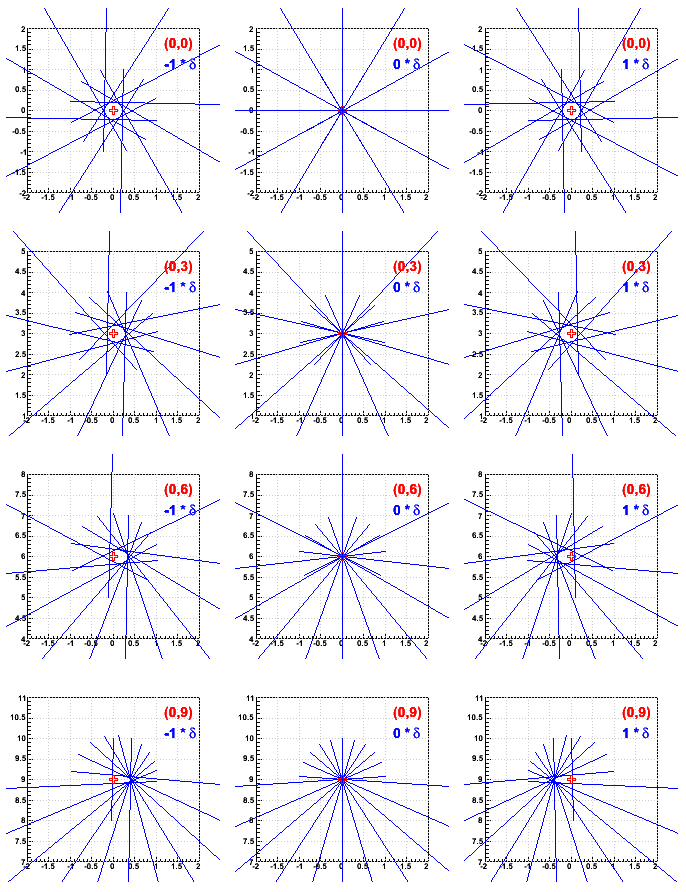
Here I demonstrate the effect in an exagerated way by using a rotation radius of 10, and primary vertex at radii of 0, 3, 6, 9, moving up the y-axis. I project tracks from 12 different azimuths back to the primary vertex, using under-corrected SC&GL distortions, no remaining distortions, and over-corrected such that the under- and over-correction leads to a rotation at the rotation radius of ±(2π)/300. The results are as shown in this matrix of plots where the row corresponds to primary vertex displacement from (0,0) (top to bottom), and the column the distortions (left to right). A red + indicates the true primary vertex position, while the would-be reconstructed primary vertex position is not actually calculated (requires doing a fit and more realistic track distributions).

Regardless, when exagerated to this degree, this model shows that the would-be reconstructed primary vertex from the distorted tracks is displaced in a tangential direction, by an amount that varies with the magnitude of the vertex displacement from (0,0) as well as the magnitude of the remaining distortion.

In conclusion, uncorrected SpaceCharge & GridLeak in the TPC will lead to displacements of reconstructed primary vertex positions, and if the error in SC&GL correction varies with luminosity, so will the displacement. This implies that BeamLine calibration will depend on SpaceCharge & GridLeak calibration. The displacement appears by eye to be more tangential with respect to (0,0) than radial, but it would require actual fits to determine to what extent the displacement is radial vs. tangential.

-Gene

p.s. I have attached a PDF of the plots, and the macro I used to create them.