Following an idea presented to me by Sergei Panitkin and Yuri Fisyak regarding possible backgrounds in the experiment hall (i.e. neutrons) which might live for something on the order of 10 seconds after the collisions that were their genesis, I looked at the measured SpaceCharge distortions in the TPC during steps in a Vernier scan taken during Run 12 pp510 operations. I used run 13109042, which had 4 sequences of stepping down the collisional luminosity by shifting the beams with respect to each other. This action is demonstrated in the following plot of BBC coincidence rate [Hz] vs. time [sec] (arbitrary time zero):

I processed several files (all 6 st_physics files with filestream 101 so that I would span the entire duration of the run) in SpaceCharge calibration mode (using tracks matched to both EMC and BTOF for pile-up exclusion) so that I could record the measured distortions as a function of time during the run, particularly the measured space charge using the track signed DCAs as an input to StMagUtilities::PredictSpaceChargeDistortion(). I did this twice, using the SpaceCharge & GridLeak distortion corrections with the current calibration, and using no distortion correction. Even if the correction is imperfect, we should be able to observe the steps at times when the luminosity changes and look for an additional lifetime component.

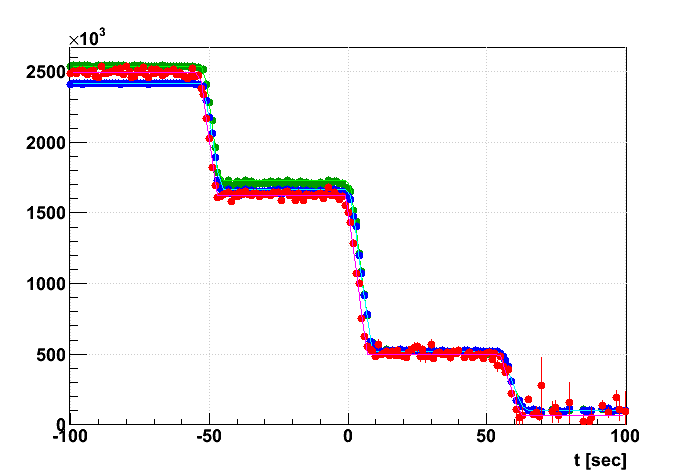
To this end, I have shifted the 4 cycles of luminosity steps so that they are overlaid to gain from the statistics, setting as t=0 the beginning of the biggest step (from ~1.6 MHz down to ~0.5 MHz). Here I show two plots for with (first) and without (second) SpaceCharge & GridLeak distortion corrections. Each plot has black lines for the BBC coincidence rate (4 lines for the 4 cycles), blue points for a profile of the BBC coincidence rates, green points for a profile of the ZDC coincidence rates, and red points for a profile of the space charge measurements:

I have arbitrarily scaled the measure of space charge and the ZDC coincidence rates such that they lie on top of the BBC coincidence rate data around t=40-50. The difference between the two plots primarily comes from the fact that without the distortion corrections, we actually lose the most distorted tracks, so the measurement of the distortion becomes biased towards the less distorted tracks, giving a smaller measured value of the distortion from the utilized ensemble of tracks. This effect gets worse with increasing distortion, to the point where the highest luminosity data on the left side of the above plot without distortion correction is completely useless.

Regardless, to the point of the exercise, we want to see if the space charge distortion takes longer to equilibrate after changes in luminosity than the ~half second it takes the primary ionization in the TPC directly from collision products to be swept out. One might come up with a more realistic function that convolutes an exponential with the shape of the luminosity determined by the scalers, but before doing anyghing like that, I have tried a simpler model to see whether there are any hints of this extended lifetime. I have fit the histograms (with distortion corrections) to 4 plateaus separated by 3 non-instantaneous "steps" which linearly drop from one plateau to the next. If the space charge has any noticeable extended lifetime, it should show up as an elongation of the steps with respect to what is seen by the scalers. Here are the results of the fit: 

Step start times and durations [sec] BBCX: -52.177 +/- 0.003 :: 6.209 +/- 0.004 0.691 +/- 0.007 :: 7.919 +/- 0.014 54.693 +/- 0.013 :: 8.895 +/- 0.034 ZDCX: -51.776 +/- 0.015 :: 5.274 +/- 0.031 0.746 +/- 0.008 :: 7.765 +/- 0.011 54.537 +/- 0.010 :: 9.358 +/- 0.059 space charge: -53.424 +/- 0.090 :: 6.088 +/- 0.165 -0.551 +/- 0.065 :: 7.431 +/- 0.134 54.861 +/- 0.316 :: 7.311 +/- 0.863

The last plot simply presents the data in the table graphically, with color codings as before. The space charge data at the lowest luminosity suffer from low statistics, and do not well constrain the 4^th plateau and the endpoint of the 3^rd step. There seems to be an elongation of steps as the luminosity drops, which I cannot say is fully understand. Angelika Drees has confirmed that 6-9 seconds is a real duration for the stepping process in the Vernier scan and writes:

'to be honest, in 1st order I don't understand why it should have 3 different times instead of 2 (since there are 2 different step sizes involved). However, the ramp time depends on what we call a "slow-factor" which is typically different for ramping up and ramping down (I know this applies to our main dipoles but I'm not certain if we do similar things with corrector magnets as well). So my best guess for what you see is that it is going "up", "down" and larger step size (i.e. 3 different times for a step). It could well be that other scans were done with a different set of slow factors and thus faster btw. Angelika'

From this data, the step duration for space charge is not significantly longer than either the ZDC or BBC coincidence rate scalers. And the lack of such probably means that this exercise was not sensitive to lifetime extensions as small as the ~half second extension which should exist (due to the time it takes ions to drift out of the TPC volume). My conclusion: the space charge measure shows no obvious lifetime components convoluting with the ~6-9 seconds it takes for the step in BBC  or ZDC rates to occur.

There is another artifact seen in the plots: an apparent time shift on the order of a second betwen the timing of the scaler rate step and the measured distortion step (the step in distortions generally comes first!). The times used in this analysis are taken directly from the header of the DAQ-recorded events. I offer two competing and real delays inherent in this:

1. The scaler rates are determined after the fact. We cannot record the scaler rate for a given one second time interval until after that time interval is over, an average is calculated, and is then delivered to the DAQ system.
2. The space charge in the TPC is the integrated result of the collisions from the (approximately) half second before any given instant.

I speculate that first of these two effects is on the order of ~1 second slower than the second (though that sounds a little bit long to me).

-Gene

p.s. I believe that a monotonic space charge distribution in the TPC cannot conspire to have no net effect on tracks' signed DCAs (e.g. some compensating push and pull), as the general trend of a shearing of reconstructed hit azimuth (effectively a rotation) would be common to all such distributions. (There is also a common compression of reconstructed hit radii which is less noticeable in track reconstruction due to their radial orientation [radial shifts in hits don't do much to a radial track], and opposing in effect on signed DCA for opposing track curvatures; i.e. some cancelation happens when using both postively and negatively charged tracks.)