- genevb's home page
- Posts
- 2025
- 2024
- 2023
- 2022
- September (1)
- 2021
- 2020
- 2019
- December (1)
- October (4)
- September (2)
- August (6)
- July (1)
- June (2)
- May (4)
- April (2)
- March (3)
- February (3)
- 2018
- 2017
- December (1)
- October (3)
- September (1)
- August (1)
- July (2)
- June (2)
- April (2)
- March (2)
- February (1)
- 2016
- November (2)
- September (1)
- August (2)
- July (1)
- June (2)
- May (2)
- April (1)
- March (5)
- February (2)
- January (1)
- 2015
- December (1)
- October (1)
- September (2)
- June (1)
- May (2)
- April (2)
- March (3)
- February (1)
- January (3)
- 2014
- December (2)
- October (2)
- September (2)
- August (3)
- July (2)
- June (2)
- May (2)
- April (9)
- March (2)
- February (2)
- January (1)
- 2013
- December (5)
- October (3)
- September (3)
- August (1)
- July (1)
- May (4)
- April (4)
- March (7)
- February (1)
- January (2)
- 2012
- December (2)
- November (6)
- October (2)
- September (3)
- August (7)
- July (2)
- June (1)
- May (3)
- April (1)
- March (2)
- February (1)
- 2011
- November (1)
- October (1)
- September (4)
- August (2)
- July (4)
- June (3)
- May (4)
- April (9)
- March (5)
- February (6)
- January (3)
- 2010
- December (3)
- November (6)
- October (3)
- September (1)
- August (5)
- July (1)
- June (4)
- May (1)
- April (2)
- March (2)
- February (4)
- January (2)
- 2009
- November (1)
- October (2)
- September (6)
- August (4)
- July (4)
- June (3)
- May (5)
- April (5)
- March (3)
- February (1)
- 2008
- 2005
- October (1)
- My blog
- Post new blog entry
- All blogs
Iterative DoDistortions in StMagUtilities
StMagUtilities corrections for distortions were implemented with the expectation that the displacements due to distortions do not vary significantly over distances comparable to those displacements. More specifically, using D(x) to denote the distortion displacement at x:
I present here some things I found using C = 1.0 micron and examining the highest luminosity good run which include the TPC (13099025), using zerobias (i.e. pile-up) data.
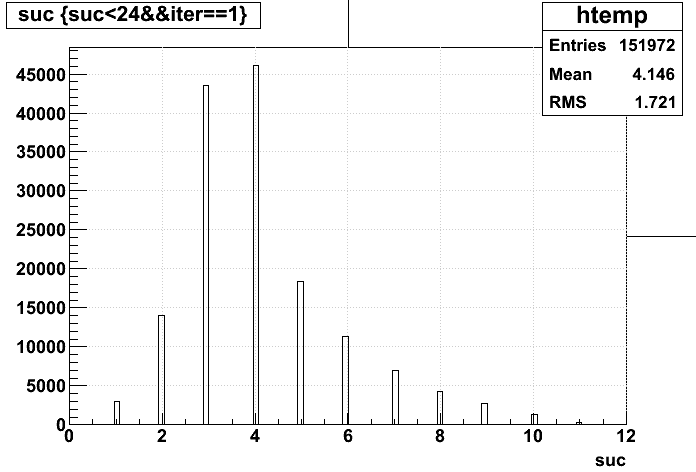
Here are the number of iterations it takes to satisfy convergence (given that it did converge); the mean number of iterations is 4.146:
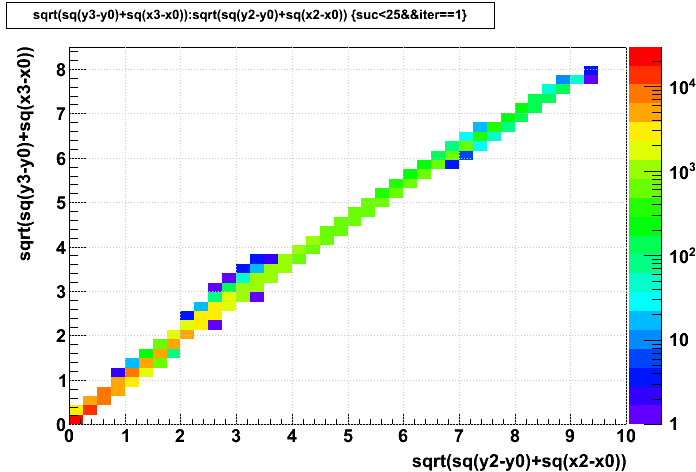
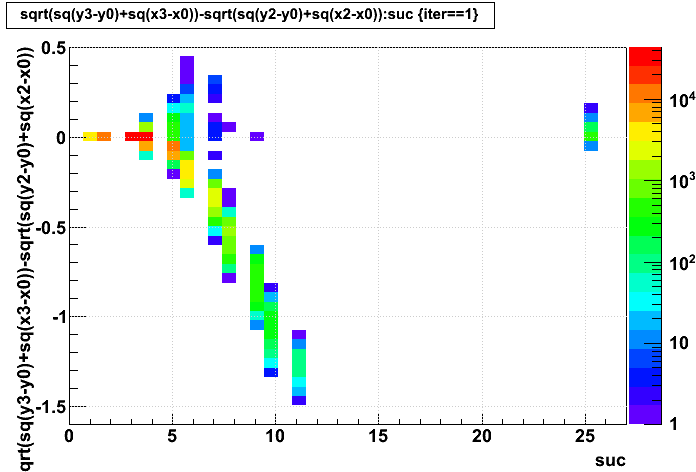
Here is the final transverse displacement after convergence vs. the displacement from the first iteration (which represents what we do now with no iteration), and then the difference in these two displacements vs. the number of iterations it took to satisfy convergence. We can see that not iterating can result in as much as a 1.5 cm error in the assigned distortion displacement, though I will note that the mean absolute error is 0.086 cm (860 microns) and the maximum error near the padrows is just below 1.0 cm (the 1.5 cm maximum is observed at radii closer to the inner field cage). There is a class of hits at 25 iterations which indicates they did not converge (I set a limit at 25).
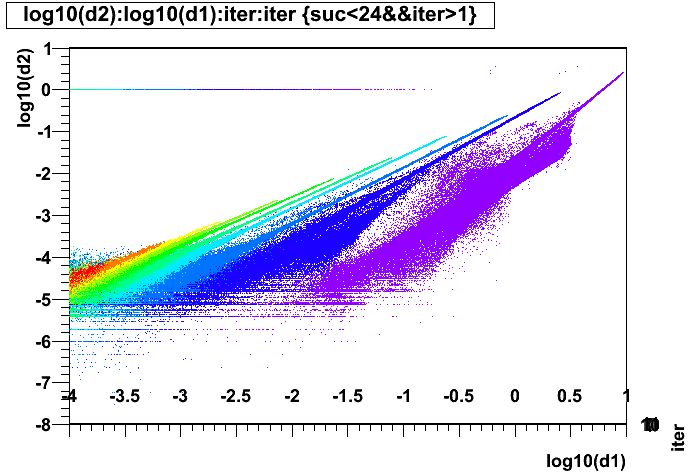
Next is what I call the "route to convergence", which shows the incremental improvement in any iteration vs. the incremental improvement of the previous iteration (essentially |x'i+1-x'i| vs. |x'i-x'i-1| ), where the color is the iteration (purple is the first iteration i=1, dark blue is i=2, etc...)
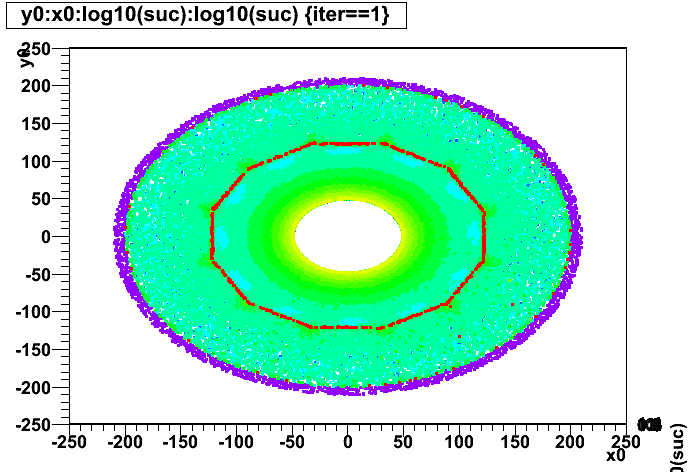
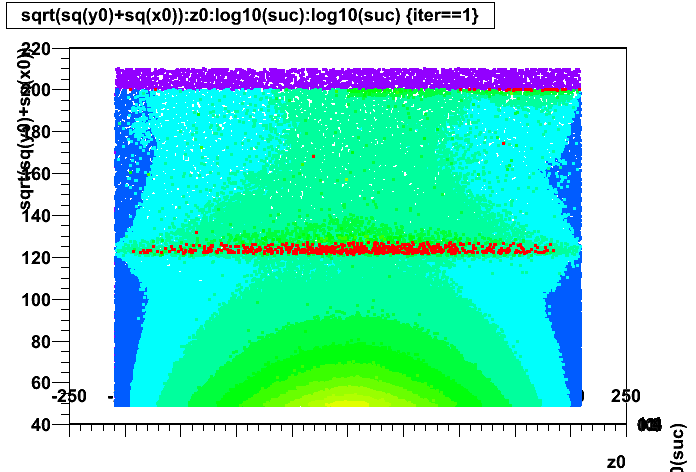
Next I try to show where in the TPC it took longest to converge, by showing y vs. x and r vs. z, using color to represent the number of iterations it took to converge (the red points are where convergence did not occur, otherwise convergence is generally quickest at the outer radii and shortest drift and slowest at the inner radii and longest drift):
Regarding the points near the GridLeak sheet of ionic charge, what appears to be happening is a back-and-forth between two positions. Here is an example:
The above example is for a hit that's moving ~1 cm between iterations for the corrected position. Among these un-converged hits, this is not extraordinary as the distance some of these hits "wobble" can be up to 3.2 cm in the data I examined.
-Gene
- if x' = x + D(x)... then D(x') = D(x)
- if x' = x + D(x)... then x = x' - D(x')
- if x' = x + D(x)... then, since we know x' a priori but not x...
- while (|D(x'i)-D(x'i-1)| > C) x'i+1 = x'0 - D(x'i)
- ...for which we expect limi→∞x'i = x {to within ~±C}
- ...allowing us to recover x = x' - D(x)
I present here some things I found using C = 1.0 micron and examining the highest luminosity good run which include the TPC (13099025), using zerobias (i.e. pile-up) data.
Here are the number of iterations it takes to satisfy convergence (given that it did converge); the mean number of iterations is 4.146:

Here is the final transverse displacement after convergence vs. the displacement from the first iteration (which represents what we do now with no iteration), and then the difference in these two displacements vs. the number of iterations it took to satisfy convergence. We can see that not iterating can result in as much as a 1.5 cm error in the assigned distortion displacement, though I will note that the mean absolute error is 0.086 cm (860 microns) and the maximum error near the padrows is just below 1.0 cm (the 1.5 cm maximum is observed at radii closer to the inner field cage). There is a class of hits at 25 iterations which indicates they did not converge (I set a limit at 25).


Next is what I call the "route to convergence", which shows the incremental improvement in any iteration vs. the incremental improvement of the previous iteration (essentially |x'i+1-x'i| vs. |x'i-x'i-1| ), where the color is the iteration (purple is the first iteration i=1, dark blue is i=2, etc...)

Next I try to show where in the TPC it took longest to converge, by showing y vs. x and r vs. z, using color to represent the number of iterations it took to converge (the red points are where convergence did not occur, otherwise convergence is generally quickest at the outer radii and shortest drift and slowest at the inner radii and longest drift):


Regarding the points near the GridLeak sheet of ionic charge, what appears to be happening is a back-and-forth between two positions. Here is an example:
| iteration | x | y | z |
|---|---|---|---|
| 0 | -3.533849 | -121.6399 | 158.79699 |
| 1 | -3.787230 | -121.833 | 158.79699 |
| 2 | -3.005870 | -121.4359 | 158.79699 |
| 3 | -3.787230 | -121.833 | 158.79699 |
| 4 | -3.005870 | -121.4359 | 158.79699 |
| ... | ... | ... | ... |
The above example is for a hit that's moving ~1 cm between iterations for the corrected position. Among these un-converged hits, this is not extraordinary as the distance some of these hits "wobble" can be up to 3.2 cm in the data I examined.
-Gene
Groups:
- genevb's blog
- Login or register to post comments
