GMT Physics Track position correlation
It is now clear to me that low ADC values correspond to correlated noise between the strips and pads. I will therefore place a cut that the product of the strip and pad ADC be greater than 1e5:
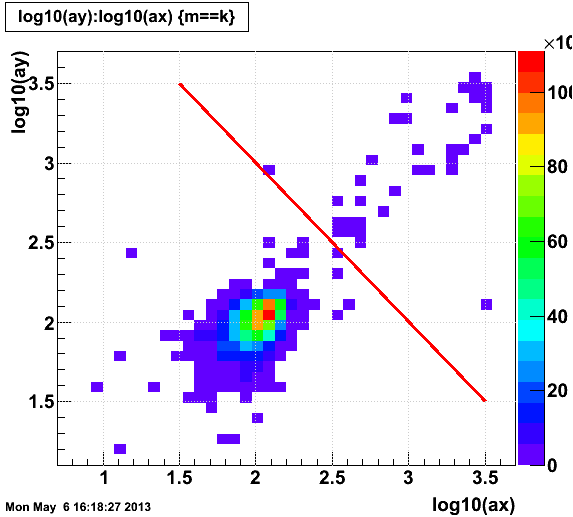
Out of 91,556 physics events that I looked at from 5 runs taken on days 108 & 109 (14108003, 14108014, 14108078, 14109021, 14109022), only 43 GMT hits survive this cut. It might also be worth noting that modules 1 through 4 (with a numbering scheme starting at 0) seem to have notably higher ADCs than the other modules, with modules 6 & 7 being particularly low.
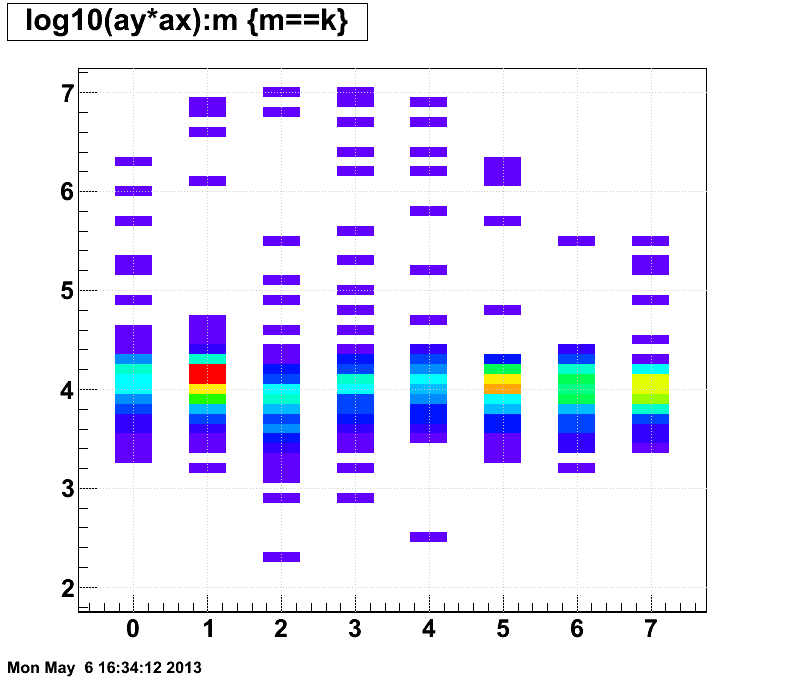
I am slightly concerned by the number of GMT hits that we are finding. Not all of the events have a GMT, so the starting point for an estimate should be the number of events which do, which in this case is 16513. The GMTs subtend (10 cm x 10 cm x 8 modules) / (2π x 217.4 cm x 400 cm) = 1.46e-3 of the surface area of the barrel. Or it can be inverted to say that 1 in every ~700 TPC tracks within |η|<1 should have a GMT hit. If I assume an average dNch/dη = 8 per event, then I expect (8 x 2 units of eta x 16513 events x 1.46e-3 GMT acceptance) = 386 GMT hits. Even if I relax my ADC cut, I'm not going to find over 100 GMT hits above the correlated noise, so the number of GMT hits is low by perhaps a little less than an order of magnitude.
Anyhow, with the ADC cut, and using global tracks with a minimum of 25 TPC hits and a maximum 3D DCA to the primary vertex of 5 cm, here are the Δ(z) vs Δ(rφ) for the 8 modules (between the GMT hit position, and the track's closest approach to that 3D point), with the 9th panel showing the sum of all 8 modules:
[NB: I have assumed ideal alignment of the GMT to the TPC, and I have accounted for the global misalignment of the TPC; I have not accounted for the non-cylindrical geometry of the GMT modules, though the effect should be small (below 1 cm).]
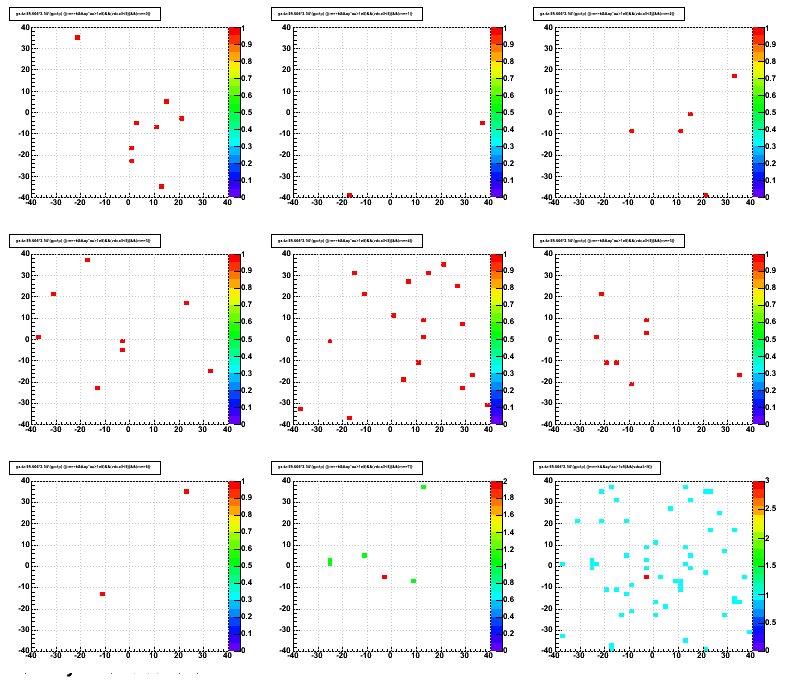
Any correlation in position here is very, very weak.
-Gene
Out of 91,556 physics events that I looked at from 5 runs taken on days 108 & 109 (14108003, 14108014, 14108078, 14109021, 14109022), only 43 GMT hits survive this cut. It might also be worth noting that modules 1 through 4 (with a numbering scheme starting at 0) seem to have notably higher ADCs than the other modules, with modules 6 & 7 being particularly low.
I am slightly concerned by the number of GMT hits that we are finding. Not all of the events have a GMT, so the starting point for an estimate should be the number of events which do, which in this case is 16513. The GMTs subtend (10 cm x 10 cm x 8 modules) / (2π x 217.4 cm x 400 cm) = 1.46e-3 of the surface area of the barrel. Or it can be inverted to say that 1 in every ~700 TPC tracks within |η|<1 should have a GMT hit. If I assume an average dNch/dη = 8 per event, then I expect (8 x 2 units of eta x 16513 events x 1.46e-3 GMT acceptance) = 386 GMT hits. Even if I relax my ADC cut, I'm not going to find over 100 GMT hits above the correlated noise, so the number of GMT hits is low by perhaps a little less than an order of magnitude.
Anyhow, with the ADC cut, and using global tracks with a minimum of 25 TPC hits and a maximum 3D DCA to the primary vertex of 5 cm, here are the Δ(z) vs Δ(rφ) for the 8 modules (between the GMT hit position, and the track's closest approach to that 3D point), with the 9th panel showing the sum of all 8 modules:
[NB: I have assumed ideal alignment of the GMT to the TPC, and I have accounted for the global misalignment of the TPC; I have not accounted for the non-cylindrical geometry of the GMT modules, though the effect should be small (below 1 cm).]
Any correlation in position here is very, very weak.
-Gene
Groups:
- genevb's blog
- Login or register to post comments