Introduction:


We have been opening the TPC gating grid (GG) at frequencies far beyond the original CDR plans of a few Hz, up into the few kHz range. This begs the question: Is this an issue for allowing ions to backflow into the TPC, as the GG was specifically designed to prevent? I was able to gather data from a database table of TCU information from Runs 11-14 (just the tail end of Run 11 and beginning of Run 14) on the GG opening frequencies. The distribution vs. year is here:


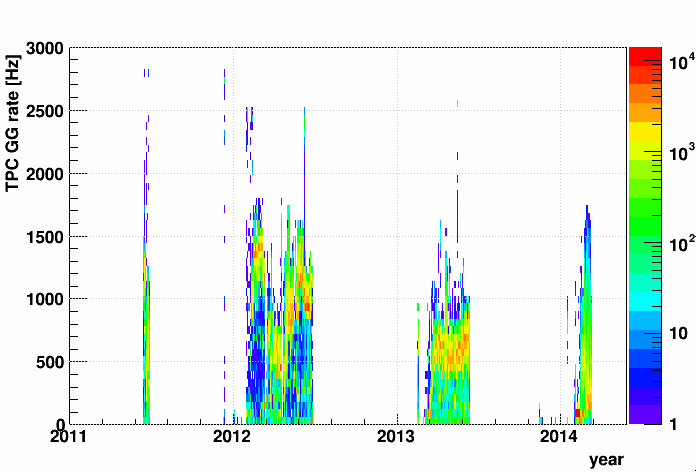
Given that we leave the GG "open" for ~50 μs at each opening, a frequency of 2000 Hz implies that the GG will be open for ~10% of the time.

The answer to the question depends on whether ions that leak out the GG (ion backflow, or IBF) rival those that are in the TPC from primary ionization ("space charge"), i.e. whether ρ_IBF / ρ_SC > ~0.1.

For every electron generated in the primary ionization of the TPC, that contributes (assuming no recombination):
ρ_SC = (1/2) * (R * L / u)
where
R : the average rate of producing electron / ion pairs per unit volume (proportional to the collision rate * average collision multiplicity * average ionization per track)
L : the full drift length
u : the ion drift velocity
(the 1/2 comes from the fact that at any given time, half the ions that have been generated in the time L/u have been swept to the cathode)

Meanwhile, the electron goes to the endcap, and must go through the gated grid, which it does at a rate O (the transparency of the grid to electrons, which is just the percentage of time the grid is open, which in our case will be 8%, or 0.08). Each electron is amplified with a gain of G = ~3000 at the anode wires, implying a release of ~3000 ions in that region. GARFIELD simulations show that most of the field lines leaving the anodes go away from the pad plane, so the gain is probably a little less, but not half that [a page on old simulations simply states qualitatively "fewer ions are expected to go toward the pad plane, and more ions are expected to go toward the ground wires"]; I will work with the worst case scenario that all field lines go away from the pad plane and all of G works against us. Of course, operating the TPC anodes at lower than designed voltages (as we've done in recent years) also helpfully reduces G.

Some of those ions may then leak out at a rate T (the transparency of the grid to the slower-moving ions). Each ion that leaks out contributes to ρ_IBF, so we find:
ρ_IBF = (O * G * T) * (R * L / u)

...and ρ_IBF/ρ_SC = 2 * O * G * T = 2 * 0.08 * 3000 * T
And we care about this if
0.1 < ρ_IBF/ρ_SC
T > 0.1 / (2 * 0.08 * 3000) = ~2e-4

So...do we care?

_________


First Approximation:


Blum, Riegler, & Rolandi ("Particle Detection with Drift Chambers", Springer, 2008) explain an approximated formula which is valid in the region of operation where the grid is macroscopically transparent to ions (Sect. 9.3.2, Eq. 9.20):

<T> = 1 - (S/s) * [2 ΔV_g / (s E_d)] (1 - f Δt)

where
<T> : average transparency
ΔV_g : voltage swing of the closed GG wires from their open state
E_d : drift E field
s : GG wire spacing pitch
S : "effective depth of the grid"
f : frequency of GG opening
Δt : duration of a single GG opening

They write that S "will be some fraction of the pitch s", and note that experiments have found values of S/s to be in the range of 0.4-0.5, putting S in the range of a few hundred μm, more than an order of magnitude shorter than the distance from the cathode to the GG of 0.6 cm. Since we're being cautious (worst case) for our calculations, I will assume that S/s = 0.4 (smaller values lead to higher transparency).

This formula essentially states that the average opacity (1 - <T>) is proportional to the fraction of time the grid is closed (1 - f Δt).

ΔV_g = 75 V
E_d = 134 V/cm
s = 0.1 cm
S/s = 0.4
f = 2000 Hz [s^-1]
Δt = 50 μs

<T> ≃ -3

This is of course non-sensical, but simply implies that we do not operate near this linear region. In order to be near that region, we would need to get <T> near zero, which would happen if we reduce what I will call the effective ΔV_g,eff = ΔV_g * (1 - f Δt) = 75 V * (1 - 0.1) = 67.5 V by another factor of ~4, such that ΔV_g,eff = 16.875 V. In other words, ΔV_g ≃ 18.75 V at the same f, or (1 - f Δt) ≃ 0.225 ⇒ f ≃ 15500 Hz at the same ΔV_g. We are certainly not in danger of reaching these operating conditions.

Blum, Riegler, & Rolandi explicitly state that any ion is absorbed by the GG, that "the transparency is zero if" the above formula returns 0 or less. Perhaps they are correct, but I find the definitiveness of this statement difficult to swallow. If it is true, then we have no problems. But the text contains the caveat that the authors "are satisfied with an order-of-magnitude calculation," as well as prefacing the calculation with the condition that:

s/u ≫ Δt

In our case, s/u is within an order of magnitude of Δt. I don't precisely know u, but my understanding is that it is believed to be on the order of ~250 cm/s for methane as the ionic charge carrier in P10 with our drift field using Fig. 2.5 of Blum, Riegler, & Rolandi section 2.2 (page 61), which suggests an inverse mobility of ~0.52 V s/cm² (P10 is 90% Ar + 10% CH₄), thus a mobility of ~1.92 cm²/V/s, multiplied by ~130 V/cm gives ~250 cm/s. Using that value of u, we get 400 μs compared to 50 μs. My guess is that this approximation likely does not precisely describe the transition from linear dependence to zero transparency, and that the transition is smooth, allowing some microscopic transparency beyond the conditions where the above formula intercepts zero. So I believe this still leaves open the question of whether we may have transparencies on the 10^-4 scale under STAR's operating conditions. Unless some other research on this is uncovered, we will likely need additional simulations to determine the answer.

__________


Simulation thoughts:


While it would be a significant task to simulate the dynamic nature of a switching GG (maybe in MAGBOLTZ?), Howard W. suggested that we could still employ the same approximation used by Blum, Riegler, & Rolandi of an effective ΔV_g,eff. This would allow a GARFIELD simulation of the E fields under the static condition of a GG in its closed state using ΔV_g,eff for the offsetting potentials on the GG wires. One could then estimate the transparency by the fraction of E field lines coming from the ground plane (cathode) which do not terminate on GG wires. This fraction could be mapped as a function of ΔV_g,eff to understand transparency in this transition region.

_________


-Gene