- genevb's home page
- Posts
- 2025
- 2024
- 2023
- 2022
- September (1)
- 2021
- 2020
- 2019
- December (1)
- October (4)
- September (2)
- August (6)
- July (1)
- June (2)
- May (4)
- April (2)
- March (3)
- February (3)
- 2018
- 2017
- December (1)
- October (3)
- September (1)
- August (1)
- July (2)
- June (2)
- April (2)
- March (2)
- February (1)
- 2016
- November (2)
- September (1)
- August (2)
- July (1)
- June (2)
- May (2)
- April (1)
- March (5)
- February (2)
- January (1)
- 2015
- December (1)
- October (1)
- September (2)
- June (1)
- May (2)
- April (2)
- March (3)
- February (1)
- January (3)
- 2014
- December (2)
- October (2)
- September (2)
- August (3)
- July (2)
- June (2)
- May (2)
- April (9)
- March (2)
- February (2)
- January (1)
- 2013
- December (5)
- October (3)
- September (3)
- August (1)
- July (1)
- May (4)
- April (4)
- March (7)
- February (1)
- January (2)
- 2012
- December (2)
- November (6)
- October (2)
- September (3)
- August (7)
- July (2)
- June (1)
- May (3)
- April (1)
- March (2)
- February (1)
- 2011
- November (1)
- October (1)
- September (4)
- August (2)
- July (4)
- June (3)
- May (4)
- April (9)
- March (5)
- February (6)
- January (3)
- 2010
- December (3)
- November (6)
- October (3)
- September (1)
- August (5)
- July (1)
- June (4)
- May (1)
- April (2)
- March (2)
- February (4)
- January (2)
- 2009
- November (1)
- October (2)
- September (6)
- August (4)
- July (4)
- June (3)
- May (5)
- April (5)
- March (3)
- February (1)
- 2008
- 2005
- October (1)
- My blog
- Post new blog entry
- All blogs
HFT material accounting in Sti (take 2)
HFT material accounting in Sti (take 2)
This is nearly for the state of the HFT materials as they were in SL14d for the April 2014 preview production. The only difference is a fix for an issue with the PXL sensitive volumes. We will further modify and improve upon these representations of the HFT geometry.
I will show here effects of adding PXL, IST, and SSD incrementally, as well as summed effects.
______________
As a metric of the effect on track projections with the accounting of material, I used <|ΔDCA|> for global tracks which had at least 25 TPC hits, 0.3 < pT < 2.0 GeV/c, and the 2D DCA to the BeamLine was within 2 cm (i.e. the track did not need to be close to a primary vertex, though the "beamline" was defined by the highest ranked primary vertex (x,y)). For the plots which use non-zero radius, I only made a correction to the z location via z + radius * (η/0.88), which is reasonable to first order for the precision of the plots I have made (the radii I used are only meant to be rough approximations for where material might be anyhow). Some additional explanations follow in the outline of what is presented:
There are a lot of plots, so please read the explanations first...
(Note: images may be opened in another browser window/tab for higher resolution, or clicked on for PDF versions. All distance units are [cm])
_______________
Let's take a closer look at the ΔDCA distributions (instead of their means)...I will exclude all unaffected tracks (ΔDCA ≡ 0)...
Here is ΔDCA vs. q/pT:
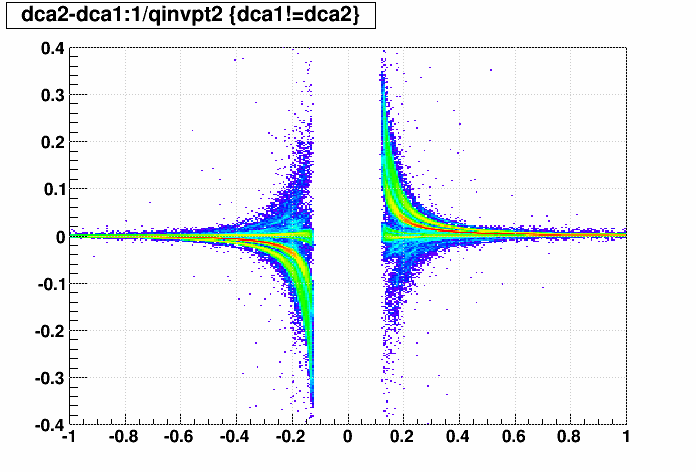
That there are bands, and where they are, makes sense. Accounting for energy loss in the track projection causes the direction of the shift to flip with charge of the track, and different materials with different densities and/or projection distances (e.g. at larger radii) will create different bands.
Multiplying ΔDCA by q*pT2 we get:
Δscaled ≡ ΔDCA * q * pT2
This makes the bands nearly flat, demonstrated in the next plot vs. log10(pT) where only the lowest pT deviate notably, providing a metric to see where material is that produces these bands:
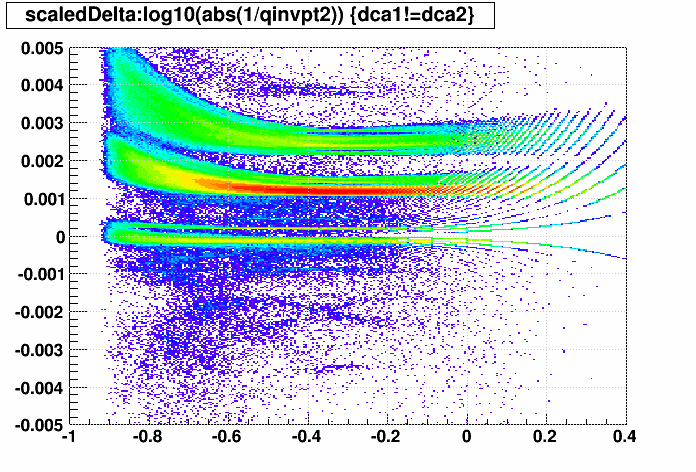
For some sense of scale, a Δscaled value of 0.0015 means that a pT = 316 MeV/c track sees a 150 μm ΔDCA, or a pT = 1 GeV/c track sees a 15 μm ΔDCA.
Accounting for energy loss means that added material will cause Δscaled to be shifted (biased) positively by an amount related to the amount of material added. On top of that there is a smearing, but I'm not 100% sure what that is (Sti's projection does not include multiple coulomb scatter).
Here are Δscaled vs. z @ r~0 cm for various material differences, where bin contents are plotted logarithmicly and normalized by the number of tracks at each z (to reduce visual effects due simply to statistics). This normalization means that the content reflects the fraction of all tracks at each z with that Δscaled value. The histogram content ranges are restricted to [0.001,0.025] to remove the statistically insignificant, while still highlighting small details. For example, solid red means that at least 2.5% of all tracks at that z have that value of dscaled, and green means ~0.5% of all tracks at that z.
I'm only showing small versions of these plots because better plots will follow:
Nothing → PXL:
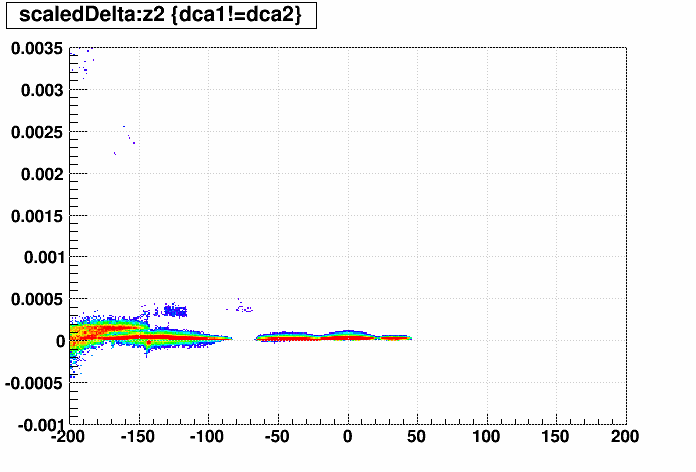
Nothing → PXL+IST and PXL → PXL+IST:


Nothing → PXL+IST+SSD and PXL+IST → PXL+IST+SSD:


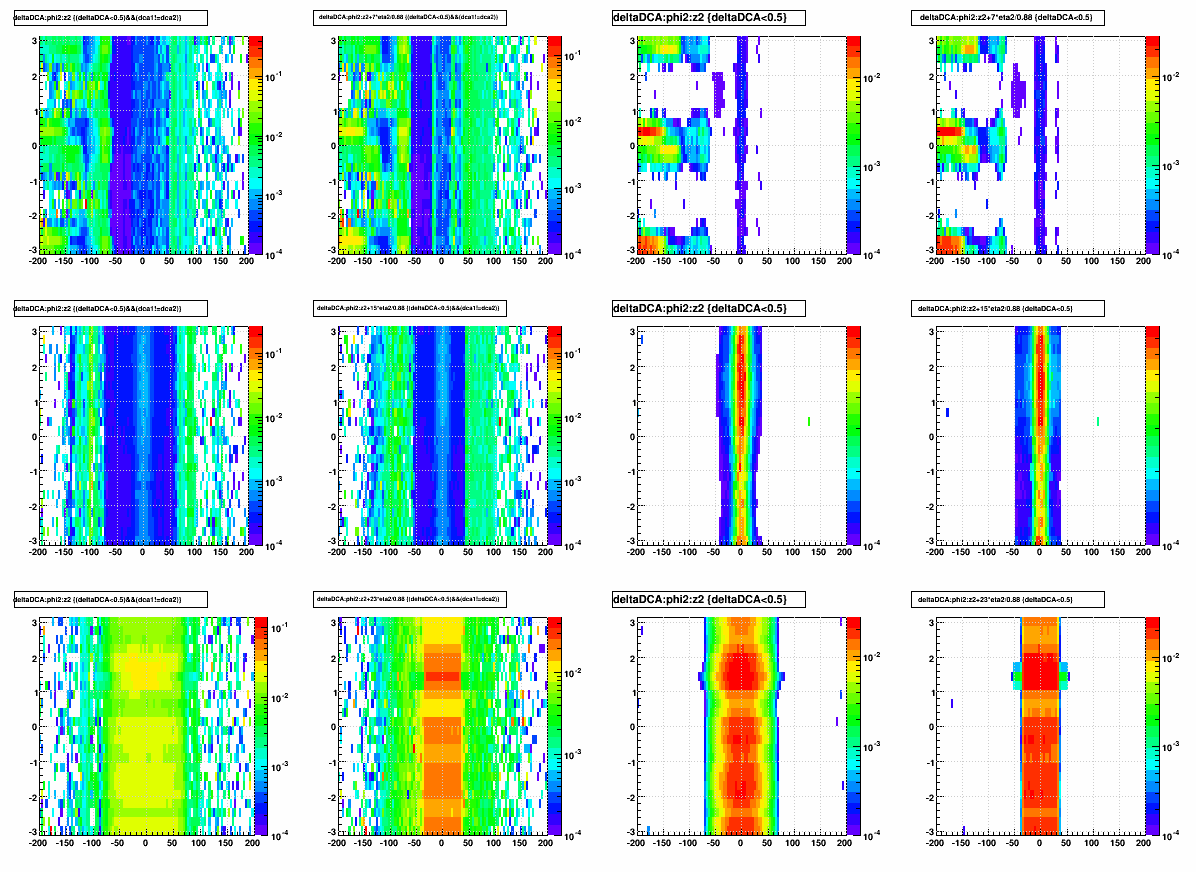
Next are the same 5 z-dependence plots, but using z @ r~7,15,23 cm for adding PXL, IST, and SSD respectively (this is of course only a rough approximation of accounting for non-zero radius and may in fact be detrimental as I don't really know at what radius the tracks intersect material [maybe at multiple radii even]). These plots are a little more "in focus", so I will show large versions:
Nothing → PXL:
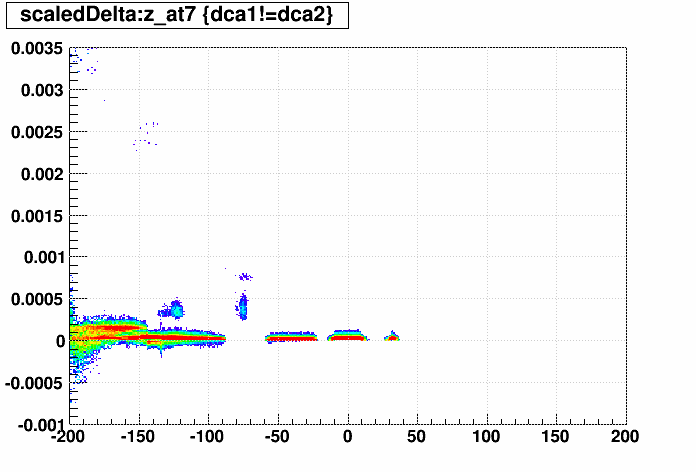
Nothing → PXL+IST and PXL → PXL+IST:


Nothing → PXL+IST+SSD and PXL+IST → PXL+IST+SSD:


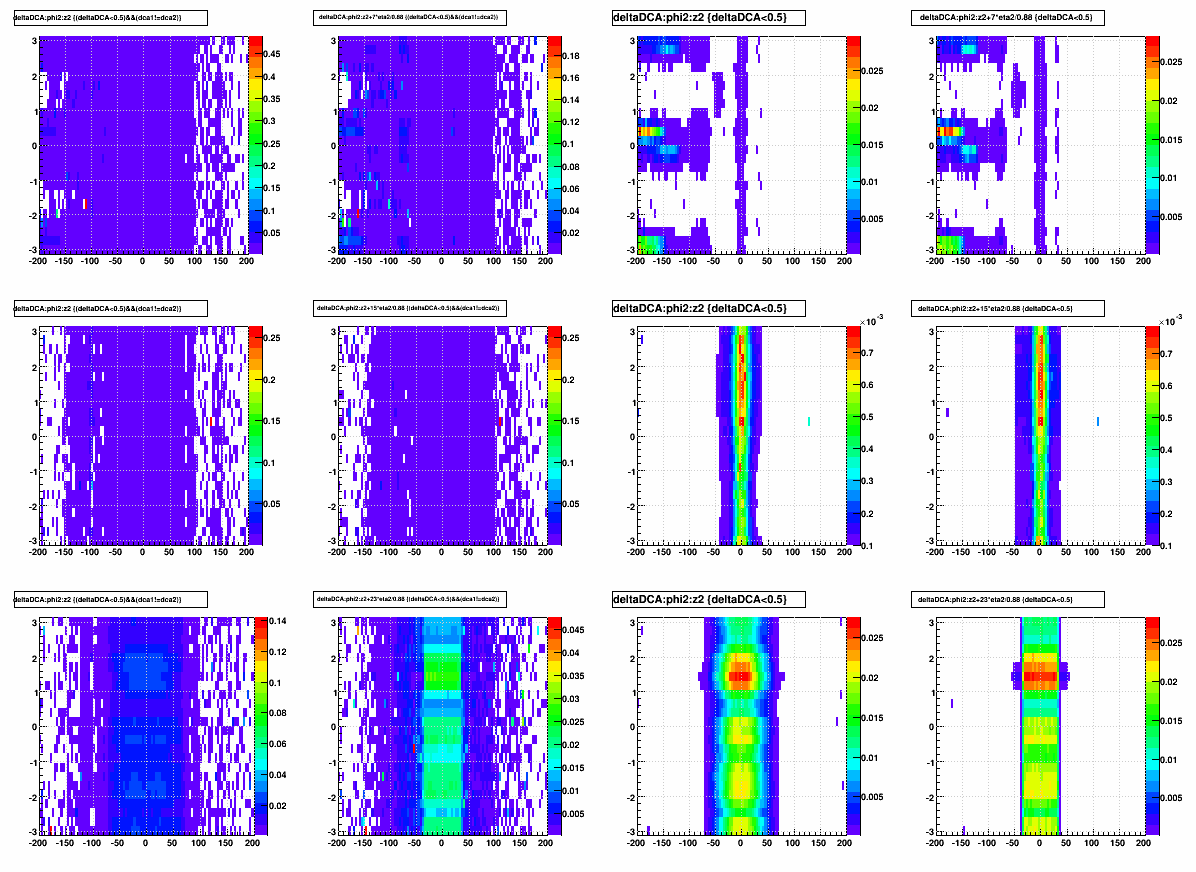
Here are the similar φ-dependence plots. I'm showing only small versions of these:
Nothing → PXL, Nothing → PXL+IST, PXL → PXL+IST, Nothing → PXL+IST+SSD, and PXL+IST → PXL+IST+SSD:





The incremental inclusion of SSD (5th plot) seems to have some rather interesting features, which can be further clarified by correcting φ for the curvature of tracks as they get out to the SSD radius: φ' = φ + 0.02*q*pT:

A better view of the smaller materials can be had using another metric, which I will call "Dmetric":
Dmetric ≡ sign(Δscaled)*(6 + log10(|Δscaled|)
Dmetric is essentially a logarithmic version of Δscaled, where 0 represents a Δscaled value of ±10-6, -1 is -10-5, +1 is 10-5, +2 is 10-4, etc. Here are the plots with z corrected for radius:
Nothing → PXL:
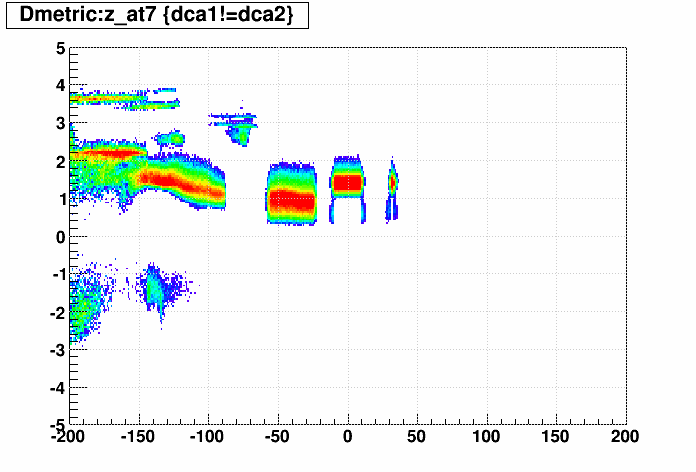
Nothing → PXL+IST and PXL → PXL+IST:


Nothing → PXL+IST+SSD and PXL+IST → PXL+IST+SSD:


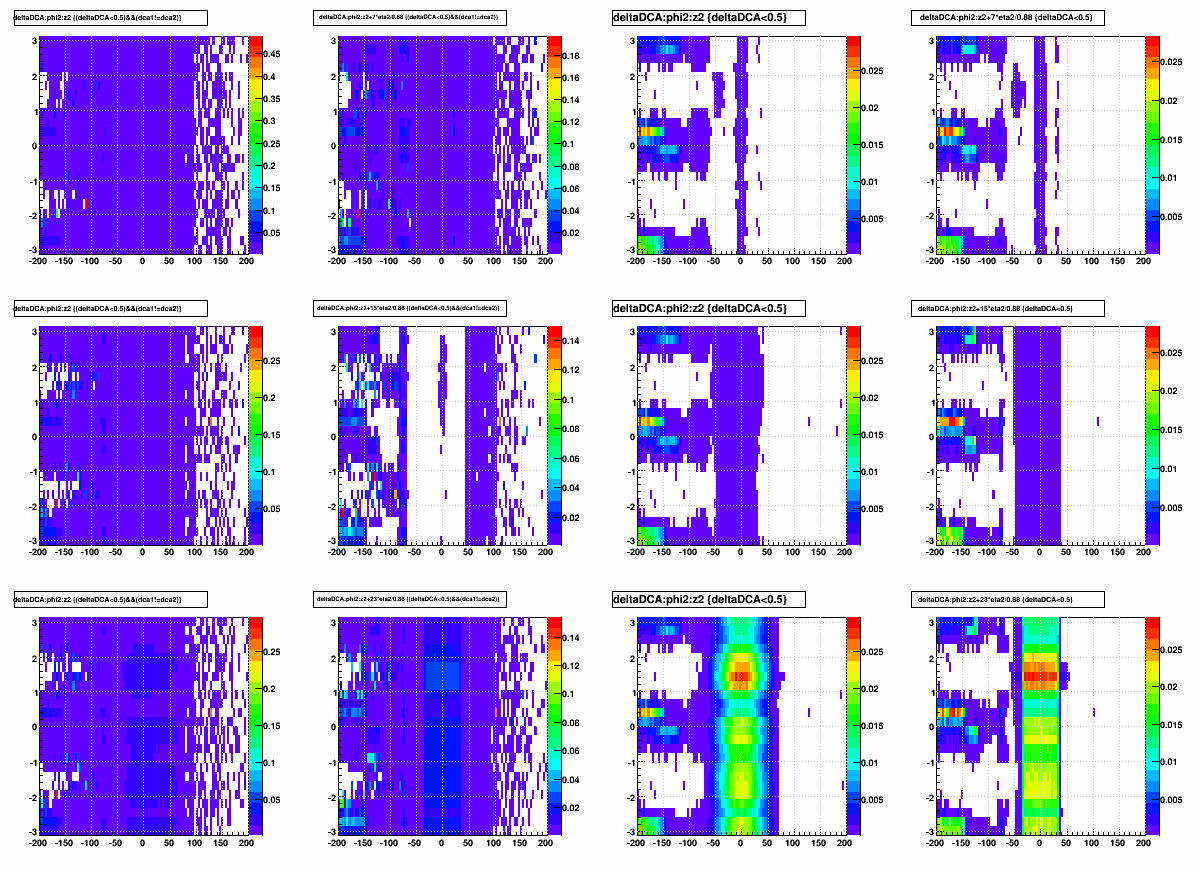
Here are the similar φ-dependence plots. I'm showing only small versions of these:
Nothing → PXL, Nothing → PXL+IST, PXL → PXL+IST, Nothing → PXL+IST+SSD, and PXL+IST → PXL+IST+SSD:
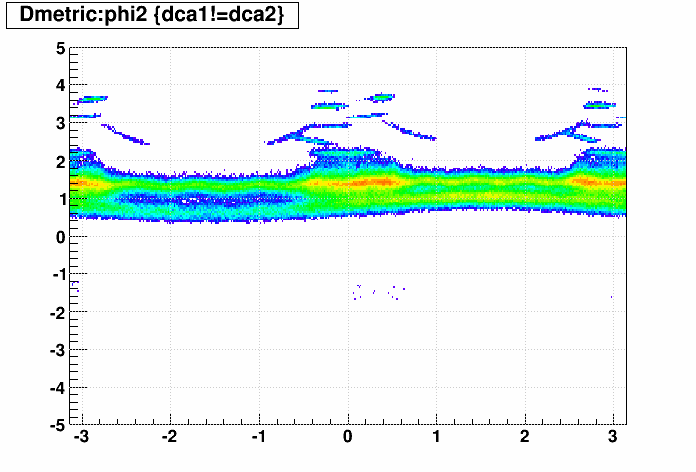




And then the incremental inclusion of SSD correction φ for curvature at the SSD using φ':

_______________
-Gene
This is nearly for the state of the HFT materials as they were in SL14d for the April 2014 preview production. The only difference is a fix for an issue with the PXL sensitive volumes. We will further modify and improve upon these representations of the HFT geometry.
I will show here effects of adding PXL, IST, and SSD incrementally, as well as summed effects.
______________
As a metric of the effect on track projections with the accounting of material, I used <|ΔDCA|> for global tracks which had at least 25 TPC hits, 0.3 < pT < 2.0 GeV/c, and the 2D DCA to the BeamLine was within 2 cm (i.e. the track did not need to be close to a primary vertex, though the "beamline" was defined by the highest ranked primary vertex (x,y)). For the plots which use non-zero radius, I only made a correction to the z location via z + radius * (η/0.88), which is reasonable to first order for the precision of the plots I have made (the radii I used are only meant to be rough approximations for where material might be anyhow). Some additional explanations follow in the outline of what is presented:
There are a lot of plots, so please read the explanations first...
- Four sets of 12 plots:
- <|ΔDCA|> when incremental materials going from (3 rows):
- Nothing → PXL
- PXL → PXL+IST
- PXL+IST → PXL+IST+SSD
- <|ΔDCA|> for summed materials going from (3 rows):
- Nothing → PXL
- Nothing → PXL+IST
- Nothing → PXL+IST+SSD
- Same as A, but plot contents are logarithmically colored
- The logarithmic scale helps obviate small-scale effects
- Same as B, but plot contents are logarithmically colored
- <|ΔDCA|> when incremental materials going from (3 rows):
- Four columns:
- <|ΔDCA|> vs. φ,z @ r~0, excluding tracks which were unaffected (ΔDCA ≡ 0)
- Exclusion of such tracks is meant to convey the affect on tracks that actually go through the material
- <|ΔDCA|> vs. φ,z @ r~7,15,23 cm respectively for the 3 rows of each of the 4 sets, excluding tracks which were unaffected
- Projecting to such radii is meant to convey more realistically the z positions of the actual materials
- <|ΔDCA|> vs. φ,z @ r~0, for all tracks, regardless of whether they were unaffected
- Inclusion of such tracks is meant to convey the total affect on tracking in general for analyses/calibrations
- <|ΔDCA|> vs. φ,z @ r~7,15,23 cm respectively for the 3 rows of each of the 4 sets, for all tracks, regardless of whether the were unaffected
- <|ΔDCA|> vs. φ,z @ r~0, excluding tracks which were unaffected (ΔDCA ≡ 0)
(Note: images may be opened in another browser window/tab for higher resolution, or clicked on for PDF versions. All distance units are [cm])
_______________
Let's take a closer look at the ΔDCA distributions (instead of their means)...I will exclude all unaffected tracks (ΔDCA ≡ 0)...
Here is ΔDCA vs. q/pT:

That there are bands, and where they are, makes sense. Accounting for energy loss in the track projection causes the direction of the shift to flip with charge of the track, and different materials with different densities and/or projection distances (e.g. at larger radii) will create different bands.
Multiplying ΔDCA by q*pT2 we get:
Δscaled ≡ ΔDCA * q * pT2
This makes the bands nearly flat, demonstrated in the next plot vs. log10(pT) where only the lowest pT deviate notably, providing a metric to see where material is that produces these bands:

For some sense of scale, a Δscaled value of 0.0015 means that a pT = 316 MeV/c track sees a 150 μm ΔDCA, or a pT = 1 GeV/c track sees a 15 μm ΔDCA.
Accounting for energy loss means that added material will cause Δscaled to be shifted (biased) positively by an amount related to the amount of material added. On top of that there is a smearing, but I'm not 100% sure what that is (Sti's projection does not include multiple coulomb scatter).
Here are Δscaled vs. z @ r~0 cm for various material differences, where bin contents are plotted logarithmicly and normalized by the number of tracks at each z (to reduce visual effects due simply to statistics). This normalization means that the content reflects the fraction of all tracks at each z with that Δscaled value. The histogram content ranges are restricted to [0.001,0.025] to remove the statistically insignificant, while still highlighting small details. For example, solid red means that at least 2.5% of all tracks at that z have that value of dscaled, and green means ~0.5% of all tracks at that z.
I'm only showing small versions of these plots because better plots will follow:
Nothing → PXL:
Nothing → PXL+IST and PXL → PXL+IST:
Nothing → PXL+IST+SSD and PXL+IST → PXL+IST+SSD:
Next are the same 5 z-dependence plots, but using z @ r~7,15,23 cm for adding PXL, IST, and SSD respectively (this is of course only a rough approximation of accounting for non-zero radius and may in fact be detrimental as I don't really know at what radius the tracks intersect material [maybe at multiple radii even]). These plots are a little more "in focus", so I will show large versions:
Nothing → PXL:

Nothing → PXL+IST and PXL → PXL+IST:


Nothing → PXL+IST+SSD and PXL+IST → PXL+IST+SSD:


Here are the similar φ-dependence plots. I'm showing only small versions of these:
Nothing → PXL, Nothing → PXL+IST, PXL → PXL+IST, Nothing → PXL+IST+SSD, and PXL+IST → PXL+IST+SSD:
The incremental inclusion of SSD (5th plot) seems to have some rather interesting features, which can be further clarified by correcting φ for the curvature of tracks as they get out to the SSD radius: φ' = φ + 0.02*q*pT:

- The 20-fold φ-segmented volumes are clearly visible.
- Something else between some of these first segments is appearing with ~2x the effect. A theory is that this is due to overlapping volumes?
- At some of these between-segment locations, the effect is completely different, causing tracks to project through the material as if they gained energy in that material instead of lost energy in it!
- There is some additional material seen in Δscaled at φ~+π/2 (straight up).
A better view of the smaller materials can be had using another metric, which I will call "Dmetric":
Dmetric ≡ sign(Δscaled)*(6 + log10(|Δscaled|)
Dmetric is essentially a logarithmic version of Δscaled, where 0 represents a Δscaled value of ±10-6, -1 is -10-5, +1 is 10-5, +2 is 10-4, etc. Here are the plots with z corrected for radius:
Nothing → PXL:

Nothing → PXL+IST and PXL → PXL+IST:


Nothing → PXL+IST+SSD and PXL+IST → PXL+IST+SSD:


Here are the similar φ-dependence plots. I'm showing only small versions of these:
Nothing → PXL, Nothing → PXL+IST, PXL → PXL+IST, Nothing → PXL+IST+SSD, and PXL+IST → PXL+IST+SSD:
And then the incremental inclusion of SSD correction φ for curvature at the SSD using φ':

_______________
-Gene
Groups:
- genevb's blog
- Login or register to post comments