Home » Groups » Spin PWG

Potential for use of kmeans-clustering for pi0/gamma discrimination

Updated on Tue, 2009-06-30 08:41. Originally created by jwebb on 2009-06-30 08:37.

Abstract: k-means clustering is used to find two smd clusters (no more, no less) in each plane associated with a gamma candidate.  The invariant mass of these clusters is reconstructed for gamma candidates above ET=4.5 GeV. 

Implementation:

foreach (gamma candidate passing a charged-particle veto) {

if ( gamma candidate ET > 4.5 GeV ) {
foreach ( smd plane ) {

seeding:
x1 = 0.5+random(0,287) // mean of cluster 1
x2 = 0.5+random(0,287) // mean of cluster 2

clustering:
foreach (smd strip) {
if ( strip closer to x1 )
add strip to cluster 1
else
add strip to cluster 2
}

iteration:
x1 = mean( cluster 1 )
x2 = mean( cluster 2 )
if ( x1 or x2 differs from last iteration )
repeat clustering
}
}
}

mean( cluster )
return energy weighted smd centroid

 
 
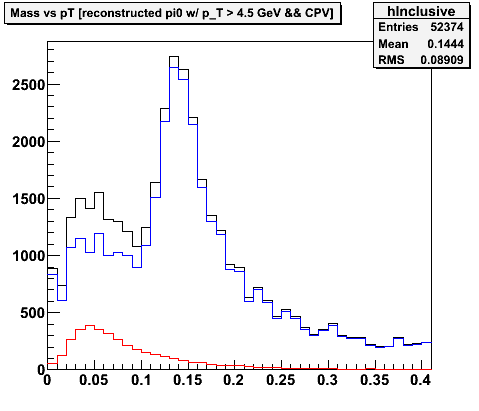
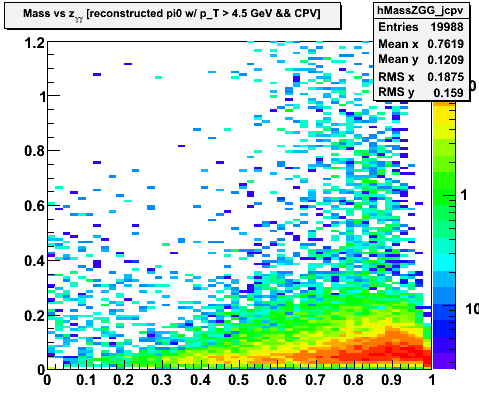
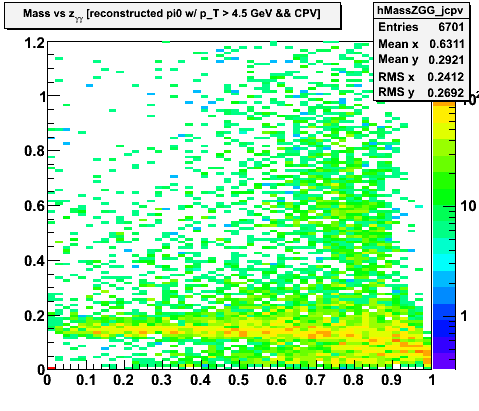
Figure 1 -- Two-cluster invariant mass distribution for Monte Carlo events.  Blue is the mit0040-45 production (jet background).  Red is the mit0034-39 production (prompt gamma).  Black is the sum of the two distributions.  

Figure 2 -- Two-cluster invariant mass plotted vs. the energy sharing (z=|E1-E2|/E) of the pair.  Left plot shows the prompt photon sample, right the jet background.  Single photons which are split tend to have large z, while diphoton candidates tend to be distributed uniformly in z at the pi0 mass. 

  1. There appears to be a substantial background from pi0 decays where one of the two photons is not found, either because it is a very high-z decay or because the 2nd photon is in an adjacent sector.
  2. I would have expected the prompt-photons to be clustered around z~0 not z~1.  Naievly I was expecting single-showers to be split into two symmetric parts.  This seems to indicate that the seeding algo is finding a bit of noise in the vicinity of the cluster, which

 Next steps:

  1. Limit seeding to +/- 40 strips from the center of the gamma candidate
  2. Implement k++ means seeding algorithm

    3. seeding:
    x1 = random( energy distribution )
    x2 = random( energy*(x-x1) distribuion )

  3. fuzzy c-means clustering

    4. clustering:
    foreach (smd strip) {
    f1 = fraction( x - x1 ) // fraction of strip belonging to cluster 1
    f2 = fraction( x - x2 ) // fraction of strip belonging to cluster 2
    }

    mean( cluster )
    return energy*f weighted smd centroid

  4. Integrate into the gamma maker for both EEMC and BEMC candidates for further study.
Groups: