Adding Landau fluctuations
Updated on Sun, 2018-04-08 07:09. Originally created by lisa on 2018-04-08 05:29.
Executive summmary
I argue that fluctuations induced by the long tail of the Landau distribution make meaningless attempts to select on very high values ADCsum in an attempt to select events with the very highest true multiplicity. This argues against lowering the gain (by lowering bias voltage on the SiPMs) of the EPD in order to retrieve any "lost information" associated with ADC values that would like to be above 4096 with present gains.
More work along these lines can and should be done to solidify (or contradict) this conclusion. Some suggestions are given at the bottom of the page.
Introduction
There has been a suggestion to lower the bias voltage on the SiPMs, in order to increase the effective dynamic range of the digitized signal from each tile. The idea is to be able to cut on more and more central collisions, avoiding tile-by-tile "saturation," in which the energy loss in the tile is restricted to a maximum ADC value of 4096. In units of the Landau Most Probable Value (MPV) of a single MIP (I'll call this MPV1), this corresponds to about 25.
There are several issues here:
The simple simulation
Here, I throw TrueMult particles and add the resulting energy loss (given by Landau distribution) to give the ADCsum. If the Landau distribution for a given particle gives a negative value, I set that contribution to 0.0. When I consider maximum ADC values below, I set the contribution to that maximum value if the Landau distribution tries to give an energy loss higher than the maximum.
If one wants to cut on simply SumAdc, one is using this as a proxy for the true multiplicity (TrueMult). I'll assume a simple "horsetail" shape to the TrueMult distribution.
In what follows, the ADC scale is defined such that ADC=1 corresponds to MPV1.
The root macro for this very simple calculation is attached here. It is not the most elegant macro, I'm afraid. Please alert me to any errors.
1) No ADC limit.
Let us first assume no limit to the measured value. This is equivalent to having an infinite-range ADC (and "perfect SiPM). . Each particle deposits energy according to the Landau distribution, and our infinite-range ADC adds up the results.
Here are the results:
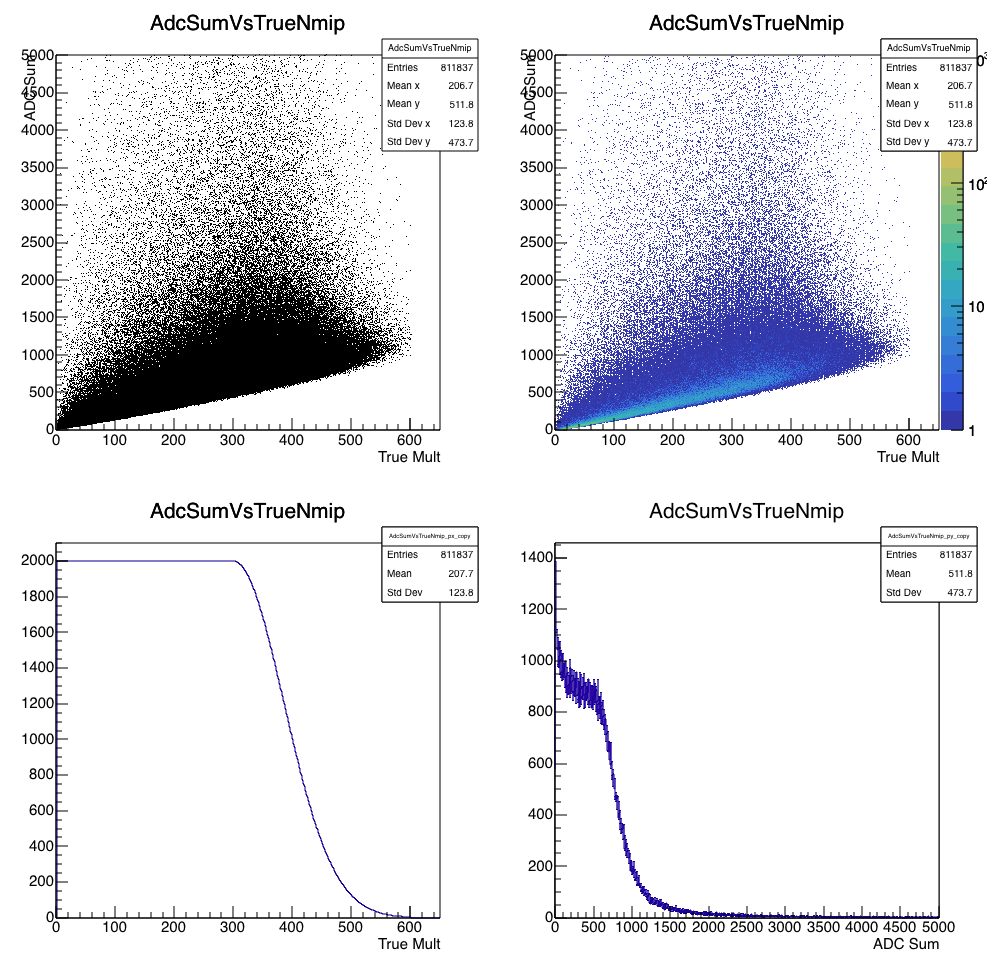
Figure 1 - Upper left and right: ADCsum versus TrueMult in linear and log Z-scales. Lower left: the "horsetail" input distribution. Lower right: the resulting ADC sum. Here, there is no upper limit on ADCsum (infinite-range ADC).
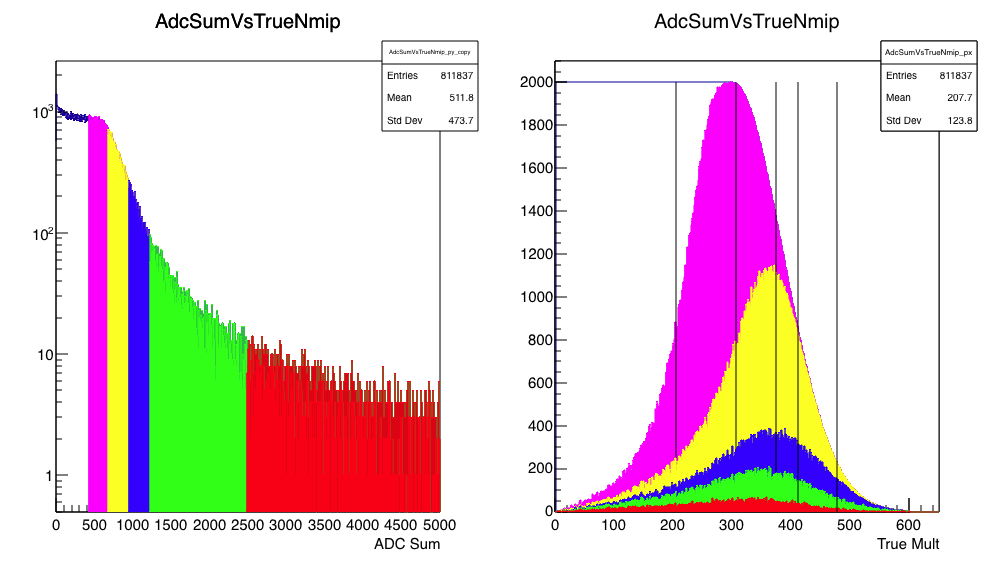
Figure 2 - Left: ADCsum distribution with 1% (red), 5% (green), 10% (blue), 25% (yellow) and 50% (magenta) cuts defined. Right: TrueMult distribution subjected to these cuts. Vertical lines show where the boundaries of (from left-most line) 50%, 25%, 10%, 5%, 1% of the TrueMult distribution.
Clearly, these cuts are not working very well! A 50% cut works okay, but things start to break down even with the 10% cut. Trying to get to 5% or 1% is clearly meaningless here.
Indeed, the 1% cut selects on average lower TrueMult events than does the 10% cut!. How can this be? Does this mean lower TrueMult collisions yield on average higher ADCsum? No, of course not. It means that high ADCsum events come on average from lower TrueMult collisions near the tail of the TrueMult distribution, simply because there are more low-TrueMult collisions. (See also my blog discussing the fact that the Landau distribution has no mean.)
2) ADC limit = 25 MPV1.
Now let us consider the case corresponding to the beginning of the 2018 run, where the max value of ADC=4096 corresponds to about 25*MPV1.
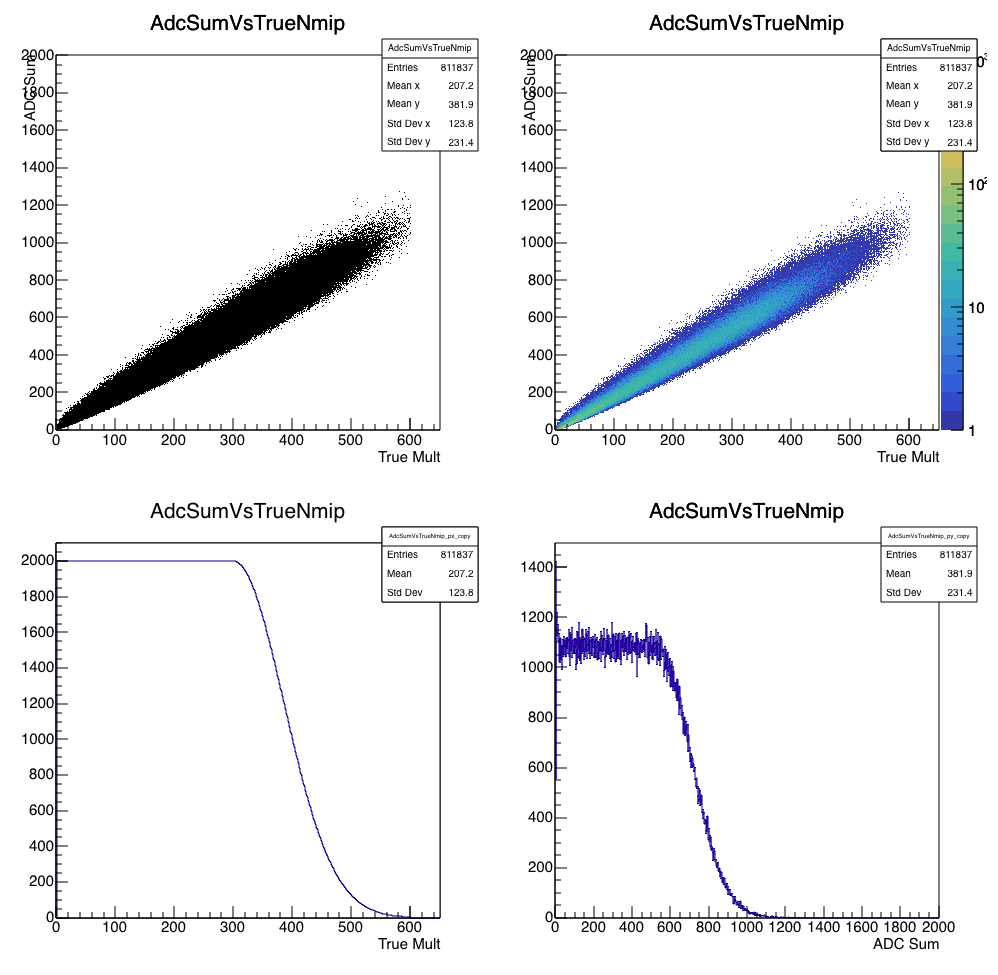
Figure 3 - Same as figure 1, but for an ADC with maximum value corresponding to 25 times the MPV of one MIP.
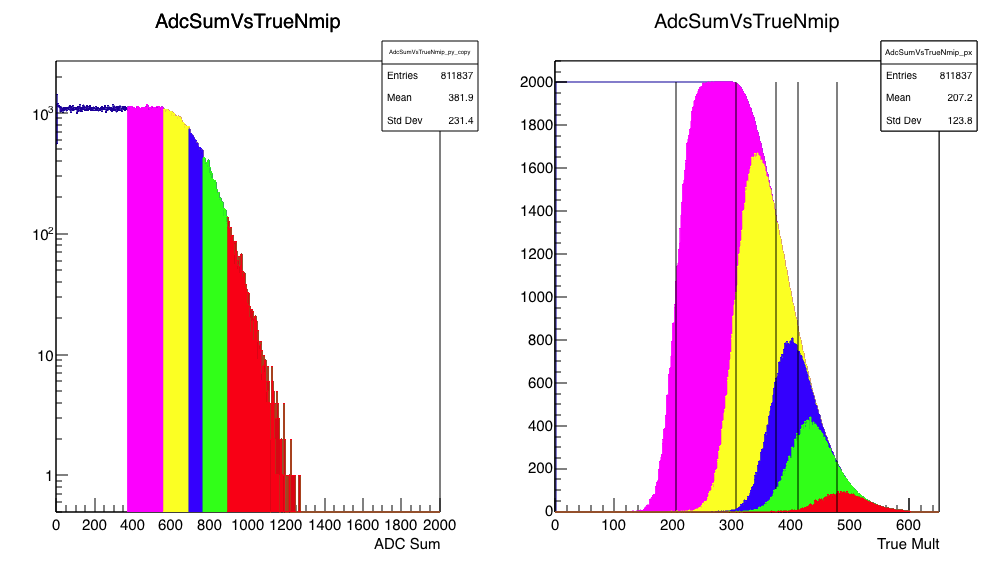
Figure 4 - Same as figure 2, but for an ADC with maximum value corresponding to 25 times the MPV of one MIP.
Well, this is much better! The 50%, 25%, and 10% cuts work pretty well, and the 5% is decent, too. The 1% cut works moderately well. Here, the maximum range of the ADC seems to be our friend!
How can this be? Aren't we "throwing away information?"
I would argue that the shape of the TrueMult distribution, coupled with the huge fluctuations induced by the long Landau tail, means that we are "throwing away meaningless noise."
3) ADC limit = 1*MPV1
What about if the ADC had a maximum range corresponding to the peak of the 1-MIP Landau distribution. (Under current EPD settings, this would be a max range around 150 ADC counts). Things seem "even better," as shown below:
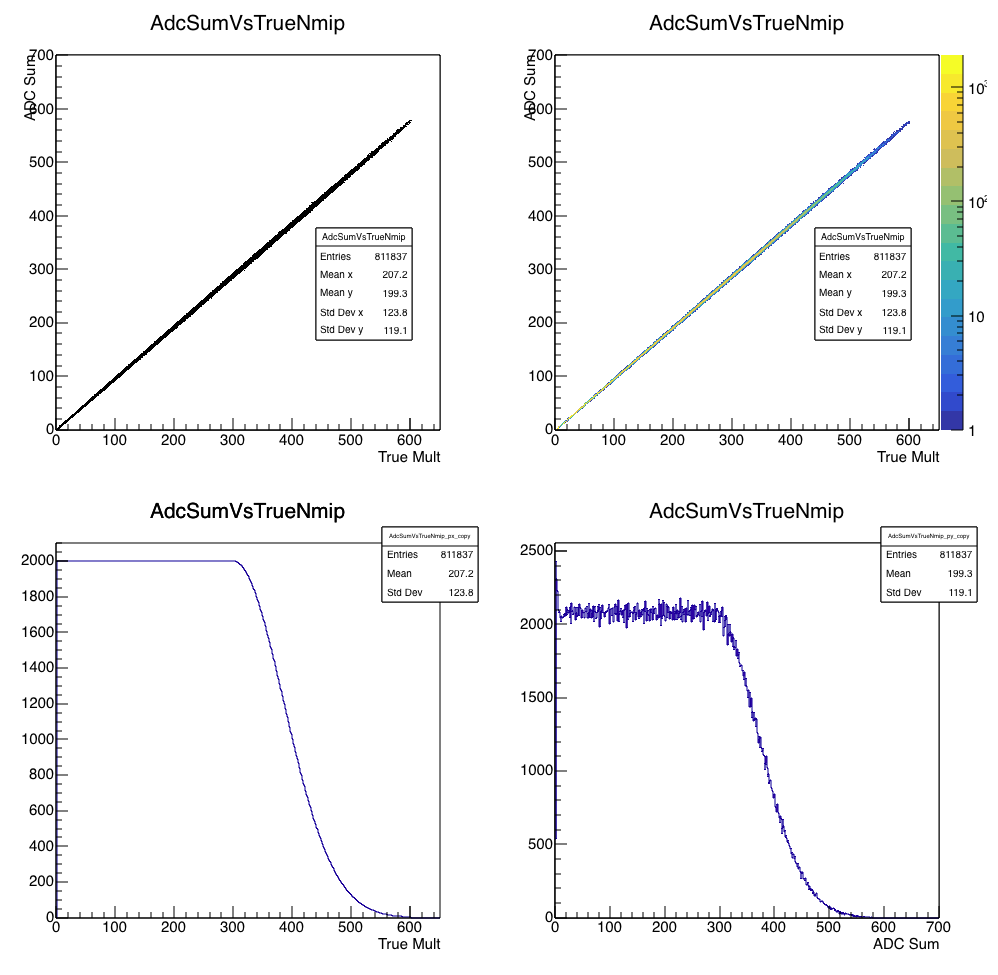
Figure 5 - Same as figures 1 and 3, but with an ADC range corresponding to the peak of the 1-MIP Landau distribution
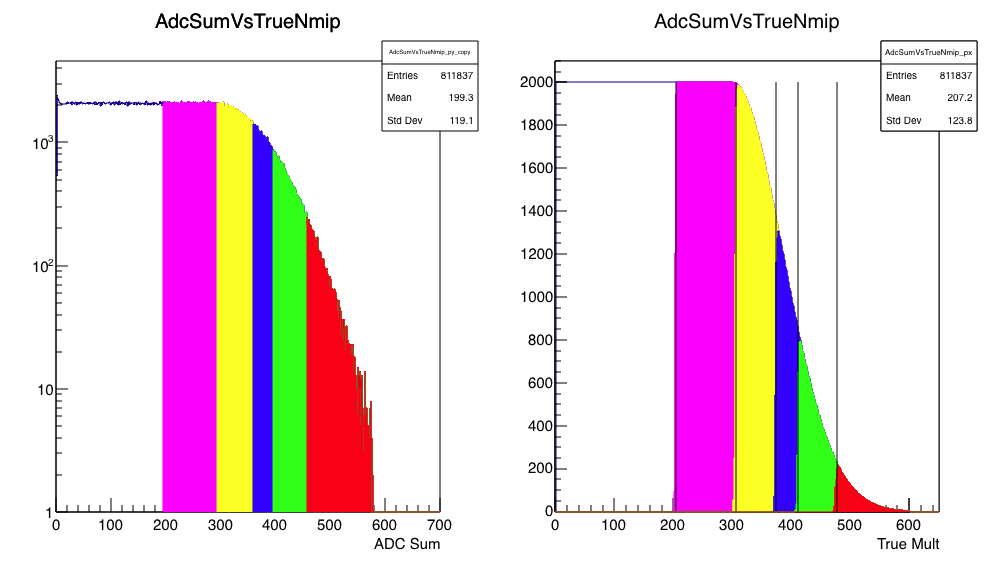
Figure 6 - Same as figures 2 and 4, but with an ADC range corresponding to the peak of the 1-MIP Landau distribution
Wait, what? Why is this happening?
In my little model, each particle is sampling the Landau distribution, the ADC limit is being applied, and then the sum added. This is equivalent to each ADC (tile) "seeing" either one or zero particles. In that case, it is not surprising that we get optimal results by treating the thing as a "hit detector." Similar to my comment above, but even more so, the Landau fluctuations are adding nothing but noise.
This situation provides a lesson: at the lower (BES) energies, we may well want to use the EPD as a hit detector. Or else set offline limits on ADC max, or something like this.
4) What next?
Case #1 discussed above (infinite-range ADC) corresponds to what ShinIchi is requesting: to lower Vbias until we never hit the ADC limit, and then using ADCsum to select event centrality. I believe I have shown that this makes little sense. Selecting events with the very highest ADCsum values will not give you the events that have the very highest TrueMult values, due to large fluctuations.
This is a fundamental limitation, quite unrelated to saturation in the SiPM or secondary scattering in detector material.
Indeed, cut-offs can be our friend.
Now then, my subsequent calculations (cases #2 and #3) are illustrative, but suffer from the assumption that the tile size is infinitely small, so that each ADC sees either zero or one MIP. A better calculation will put varying number (Poisson distribution?) of MIPs through a tile, and then limit the ADC range, and then add up tiles calculate the ADCsum. Better yet, a Geant calculation.
I believe, since we simply do not regularly have 5 or more particles passing through on tile, that relaxing this assumption would change the conclusion. But I have not calculated that.
I invite somebody (else) to pursue this or a similar calculation, to help make the case that we should lower our gains.
I argue that fluctuations induced by the long tail of the Landau distribution make meaningless attempts to select on very high values ADCsum in an attempt to select events with the very highest true multiplicity. This argues against lowering the gain (by lowering bias voltage on the SiPMs) of the EPD in order to retrieve any "lost information" associated with ADC values that would like to be above 4096 with present gains.
More work along these lines can and should be done to solidify (or contradict) this conclusion. Some suggestions are given at the bottom of the page.
Introduction
There has been a suggestion to lower the bias voltage on the SiPMs, in order to increase the effective dynamic range of the digitized signal from each tile. The idea is to be able to cut on more and more central collisions, avoiding tile-by-tile "saturation," in which the energy loss in the tile is restricted to a maximum ADC value of 4096. In units of the Landau Most Probable Value (MPV) of a single MIP (I'll call this MPV1), this corresponds to about 25.
There are several issues here:
- It has been pointed out that there is a limitation and nonlinearity due to the fact that the SiPM has only about 1600 illuminated pixels. In this case, one might expect some "saturation" effects at about 10 MPV1.
- There is also the question whether there is any physical reason to cut on ever-smaller (0.01%, anyone?) centrality selections. However, one never knows what the theorists will come up with in future, so we'd like to have data on tape.
- There is also significant secondary contributions to the signal. About half of the particles passing through the EPD are from scattering in material on the way to the detector. This is not simply a "multiplier," but also a source of fluctuation. Cutting at the 0.01% level is probably in the fluctuation.
The simple simulation
Here, I throw TrueMult particles and add the resulting energy loss (given by Landau distribution) to give the ADCsum. If the Landau distribution for a given particle gives a negative value, I set that contribution to 0.0. When I consider maximum ADC values below, I set the contribution to that maximum value if the Landau distribution tries to give an energy loss higher than the maximum.
If one wants to cut on simply SumAdc, one is using this as a proxy for the true multiplicity (TrueMult). I'll assume a simple "horsetail" shape to the TrueMult distribution.
In what follows, the ADC scale is defined such that ADC=1 corresponds to MPV1.
The root macro for this very simple calculation is attached here. It is not the most elegant macro, I'm afraid. Please alert me to any errors.
1) No ADC limit.
Let us first assume no limit to the measured value. This is equivalent to having an infinite-range ADC (and "perfect SiPM). . Each particle deposits energy according to the Landau distribution, and our infinite-range ADC adds up the results.
Here are the results:

Figure 1 - Upper left and right: ADCsum versus TrueMult in linear and log Z-scales. Lower left: the "horsetail" input distribution. Lower right: the resulting ADC sum. Here, there is no upper limit on ADCsum (infinite-range ADC).

Figure 2 - Left: ADCsum distribution with 1% (red), 5% (green), 10% (blue), 25% (yellow) and 50% (magenta) cuts defined. Right: TrueMult distribution subjected to these cuts. Vertical lines show where the boundaries of (from left-most line) 50%, 25%, 10%, 5%, 1% of the TrueMult distribution.
Clearly, these cuts are not working very well! A 50% cut works okay, but things start to break down even with the 10% cut. Trying to get to 5% or 1% is clearly meaningless here.
Indeed, the 1% cut selects on average lower TrueMult events than does the 10% cut!. How can this be? Does this mean lower TrueMult collisions yield on average higher ADCsum? No, of course not. It means that high ADCsum events come on average from lower TrueMult collisions near the tail of the TrueMult distribution, simply because there are more low-TrueMult collisions. (See also my blog discussing the fact that the Landau distribution has no mean.)
2) ADC limit = 25 MPV1.
Now let us consider the case corresponding to the beginning of the 2018 run, where the max value of ADC=4096 corresponds to about 25*MPV1.

Figure 3 - Same as figure 1, but for an ADC with maximum value corresponding to 25 times the MPV of one MIP.

Figure 4 - Same as figure 2, but for an ADC with maximum value corresponding to 25 times the MPV of one MIP.
Well, this is much better! The 50%, 25%, and 10% cuts work pretty well, and the 5% is decent, too. The 1% cut works moderately well. Here, the maximum range of the ADC seems to be our friend!
How can this be? Aren't we "throwing away information?"
I would argue that the shape of the TrueMult distribution, coupled with the huge fluctuations induced by the long Landau tail, means that we are "throwing away meaningless noise."
3) ADC limit = 1*MPV1
What about if the ADC had a maximum range corresponding to the peak of the 1-MIP Landau distribution. (Under current EPD settings, this would be a max range around 150 ADC counts). Things seem "even better," as shown below:

Figure 5 - Same as figures 1 and 3, but with an ADC range corresponding to the peak of the 1-MIP Landau distribution

Figure 6 - Same as figures 2 and 4, but with an ADC range corresponding to the peak of the 1-MIP Landau distribution
Wait, what? Why is this happening?
In my little model, each particle is sampling the Landau distribution, the ADC limit is being applied, and then the sum added. This is equivalent to each ADC (tile) "seeing" either one or zero particles. In that case, it is not surprising that we get optimal results by treating the thing as a "hit detector." Similar to my comment above, but even more so, the Landau fluctuations are adding nothing but noise.
This situation provides a lesson: at the lower (BES) energies, we may well want to use the EPD as a hit detector. Or else set offline limits on ADC max, or something like this.
4) What next?
Case #1 discussed above (infinite-range ADC) corresponds to what ShinIchi is requesting: to lower Vbias until we never hit the ADC limit, and then using ADCsum to select event centrality. I believe I have shown that this makes little sense. Selecting events with the very highest ADCsum values will not give you the events that have the very highest TrueMult values, due to large fluctuations.
This is a fundamental limitation, quite unrelated to saturation in the SiPM or secondary scattering in detector material.
Indeed, cut-offs can be our friend.
Now then, my subsequent calculations (cases #2 and #3) are illustrative, but suffer from the assumption that the tile size is infinitely small, so that each ADC sees either zero or one MIP. A better calculation will put varying number (Poisson distribution?) of MIPs through a tile, and then limit the ADC range, and then add up tiles calculate the ADCsum. Better yet, a Geant calculation.
I believe, since we simply do not regularly have 5 or more particles passing through on tile, that relaxing this assumption would change the conclusion. But I have not calculated that.
I invite somebody (else) to pursue this or a similar calculation, to help make the case that we should lower our gains.
»
- lisa's blog
- Login or register to post comments
