Fit method versus ADC-weighted, revisited
Updated on Tue, 2017-07-11 19:50. Originally created by lisa on 2017-07-11 10:01.
At the EPD meeting on 10 July 2017, Kazuma made a nice presentation and it led to a discussion about the validity of the "fit method" (see https://drupal.star.bnl.gov/STAR/blog/lisa/measuring-pseudorapidity-distribution-epd) versus the "ADC-weighted" method, for extracting v2 and dN/deta from the EPD.
I believe we can all agree that any such analysis should cut on overall multiplicity (e.g. refMult, but it could be something else) and primary vertex position. If we talk about v2 in terms of finding the event plane with the TPC, and looking at the azimuthal dependence of the particle flux relative to that plane, then in all cases we are basically interested in the average (over events, and within a multiplicity, Vz, and phi-PhiRP bin) number of particles going through a given tile, <N>. (And then we combine the tile and Vz information in a straightforward way.)
In the "fit method," one fits the ADC distribution to extract the fraction, fN, of zero-MIP, 1-MIP, 2-MIP, .... N-MIP events, and then the average number of particles per event is
.png)
In the "ADC method," one assumes that the average number of particles passing through the detector per event <N> is proportional to the average ADC value.
.png)
Here, Ncounts(ADC) is simply the ADC distribution. If it is a root TH1, then <N> is simply proportional to hist->GetMean().
ShinIchi argued that for some event-average quantities (such as <N>), the ADC-weighting method should be valid. I argued that one cannot make a definite connection between ADC and NMIP, even on average, without knowing the fN values (which are also event-average quantities). This statement of mine is correct, but
I have done a short study that supports ShinIchi's claim. But there are important caveats, which I think ShinIchi will agree with.
The energy loss in our scintillators follows a Landau distribution, and the ADC spectra that we observe follows this distribution to an astonishingly (to me) extent. In principle, one should convolute this with a Poisson distribution to account for finite photon statistics, but we have shown that this is very small for our detector, due to the (thankfully) high photon rate. The entire ADC distribution for one tile is dictated by
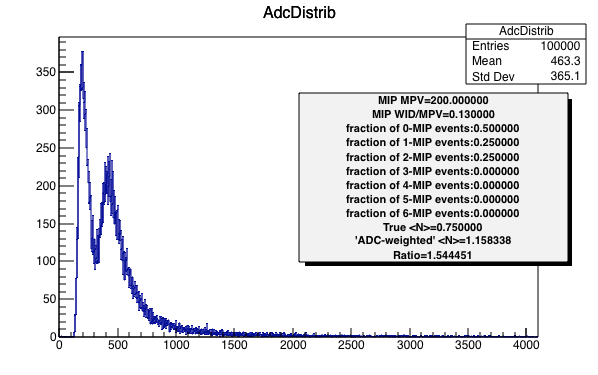
Below, I show simulated ADC spectra where the single-MIP MPV is 200 ADC counts, and WID/MPV=0.13. I play with the fN and include unrealistic cases. One sees that there is a nearly constant (within a few percent) proportionality between the true <N> and the ADC average divided by MPV, for arbitrary fN. ("Ratio" is about 1.5 in this case, though there is a small and systematic variation depending on the fraction of multi-MIP events.)
.png)
.png)
.png)
So, it seems that one must simply divide by about 1.5, and you get the "true" <N>!
Very good. But a caveat: the proportionality constant is not always 1.5, but depends on the width parameter WID. For a very narrow Landau, the proportionality is 1.0, as expected and shown below:
.png)
.png)
And for very wide Landau, the factor is larger than 1.5, as shown below:
.png)
.png)
The reason I point out the WID-dependence of the proportionality, is that WID/MPV will itself vary with the angle that the particle passes through the tile (i.e. eta). Passing through more plastic will reduce WID/MPV. And we recall that even for a given tile, eta itself depends on Vz. Therefore, before applying ADC-weighting method, a study of WID will need to be done. Also, a determination of MPV, tile-by-tile and Vz-by-Vz will need to be done. This study should be done by fitting the spectra. It should not be hard, and I expect the dependences to be mild.
Conclusions:
I believe we can all agree that any such analysis should cut on overall multiplicity (e.g. refMult, but it could be something else) and primary vertex position. If we talk about v2 in terms of finding the event plane with the TPC, and looking at the azimuthal dependence of the particle flux relative to that plane, then in all cases we are basically interested in the average (over events, and within a multiplicity, Vz, and phi-PhiRP bin) number of particles going through a given tile, <N>. (And then we combine the tile and Vz information in a straightforward way.)
In the "fit method," one fits the ADC distribution to extract the fraction, fN, of zero-MIP, 1-MIP, 2-MIP, .... N-MIP events, and then the average number of particles per event is
.png)
In the "ADC method," one assumes that the average number of particles passing through the detector per event <N> is proportional to the average ADC value.
.png)
Here, Ncounts(ADC) is simply the ADC distribution. If it is a root TH1, then <N> is simply proportional to hist->GetMean().
ShinIchi argued that for some event-average quantities (such as <N>), the ADC-weighting method should be valid. I argued that one cannot make a definite connection between ADC and NMIP, even on average, without knowing the fN values (which are also event-average quantities). This statement of mine is correct, but
- one usually does not really care what the fN values are.
- this does not necessarily invalidate the ADC-weighting method.
I have done a short study that supports ShinIchi's claim. But there are important caveats, which I think ShinIchi will agree with.
The energy loss in our scintillators follows a Landau distribution, and the ADC spectra that we observe follows this distribution to an astonishingly (to me) extent. In principle, one should convolute this with a Poisson distribution to account for finite photon statistics, but we have shown that this is very small for our detector, due to the (thankfully) high photon rate. The entire ADC distribution for one tile is dictated by
- Landau single-MIP MPV, which may be expressed in ADC counts thanks to the excellent linearity of the FEEs and QT ADCs
- Landau single-MIP WID/MPV, which is about 0.13 for scintillators of our type and thickness
- the fN values
Below, I show simulated ADC spectra where the single-MIP MPV is 200 ADC counts, and WID/MPV=0.13. I play with the fN and include unrealistic cases. One sees that there is a nearly constant (within a few percent) proportionality between the true <N> and the ADC average divided by MPV, for arbitrary fN. ("Ratio" is about 1.5 in this case, though there is a small and systematic variation depending on the fraction of multi-MIP events.)

.png)
.png)
.png)
So, it seems that one must simply divide by about 1.5, and you get the "true" <N>!
Very good. But a caveat: the proportionality constant is not always 1.5, but depends on the width parameter WID. For a very narrow Landau, the proportionality is 1.0, as expected and shown below:
.png)
.png)
And for very wide Landau, the factor is larger than 1.5, as shown below:
.png)
.png)
The reason I point out the WID-dependence of the proportionality, is that WID/MPV will itself vary with the angle that the particle passes through the tile (i.e. eta). Passing through more plastic will reduce WID/MPV. And we recall that even for a given tile, eta itself depends on Vz. Therefore, before applying ADC-weighting method, a study of WID will need to be done. Also, a determination of MPV, tile-by-tile and Vz-by-Vz will need to be done. This study should be done by fitting the spectra. It should not be hard, and I expect the dependences to be mild.
Conclusions:
- dN/deta and v2 require <N>, the event-average number of MIPs that pass through a tile, for a given multiplicity, Vz and phi relative to EP.
- The ADC-weighted method is valid, to within a few percent, to extract <N>, and it is a lot easier than the fitting method.
- The ADC-weighted method requires determination of MPV and WID for each tile for each Vz. These values should be determined by fitting.
- The ADC-weighted method is not useful to extract fN, the event-weighted proportion of N-MIP events in the tile. However, while a study of fN is important to make sure we understand the data, it is not a necessary input for dN/deta or v2 analyses.
»
- lisa's blog
- Login or register to post comments
