Optimizing EP[1] resolution in Au27Au: From ring-dependent weights to eta-dependent weights
Updated on Wed, 2018-10-24 15:57. Originally created by lisa on 2018-06-08 09:38.
Go to update posted 24 Oct 2018 - 1st-order EP resolution with and without eta weights
Executive summary:
I have shown previously the importance of giving different EPD rings "weights," when finding the first-order event plane in Au+Au collisions at 27 GeV. As I said (as did Gang Wang), the weights should in principle depend on eta, not weight. A natural weighting would be the v1 signal itself (though it may not be the best, as net flux depends on eta, too, and could be part of the equation as well.)
Here, I find that weighting with centrality- and eta-dependent v1 gives basically the same result as weighting with the centrality-independent and ring-dependent values that were originally optimized for 10-40% centrality.
Going forward, it is probably best to switch to the v1(centrality,eta) weights, since they are more likely to be robust against primary vertex fluctuations, though this will need to be confirmed.
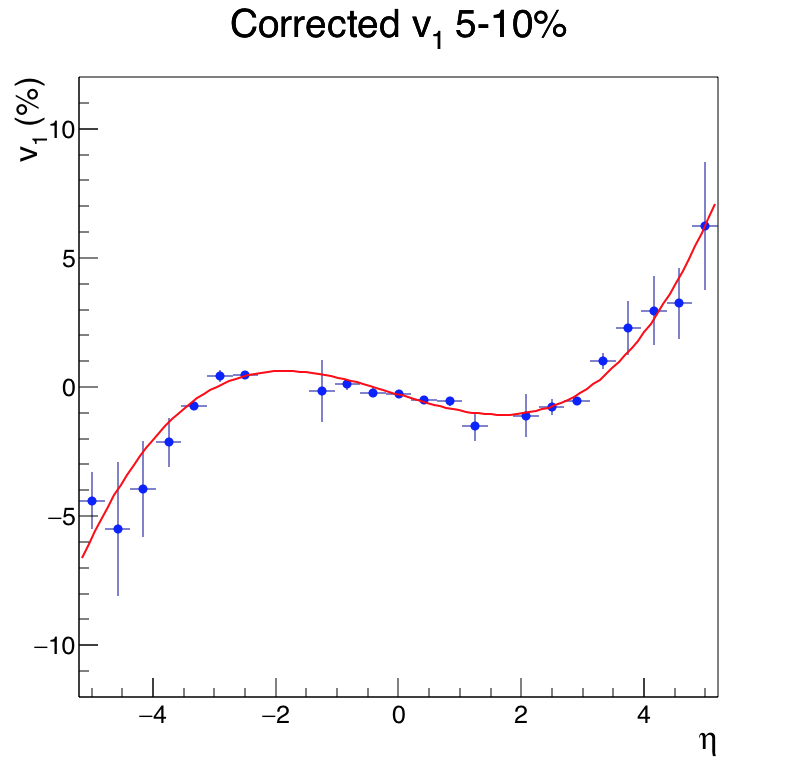
The directed flow depends on eta and on centrality. Capturing all of this dependence to generate weights is much easier if we fit the eta dependence, and then have the fit parameters depend on centrality bin. This turns out to be quite easy. Here are cubic ("pol3") fits to v1-versus-eta. The quadratic coefficient is always consistent with zero. The constant term is always a little bit negative (as I've mentioned before), but is insignificant here so I ignore it.
Except for the 0-5% bin, where the v1 determination doesn't converge well (I'm sure I could fix it if I put in the effort but not now), a cubic fit represents the data perfectly. Certainly good enough for our purposes.
.png)
.png)
.png)
.png)
.png)
.png)
.png)
Figures 1-8: Corrected v1 in eight centrality bins (0-5% has problems so not shown), with a cubic fit. Only the x and x3 terms are important.
Here are the fit parameters themselves, as a function of "centID". centID=0 means 70-80%. CentID=8 means 0-5%.
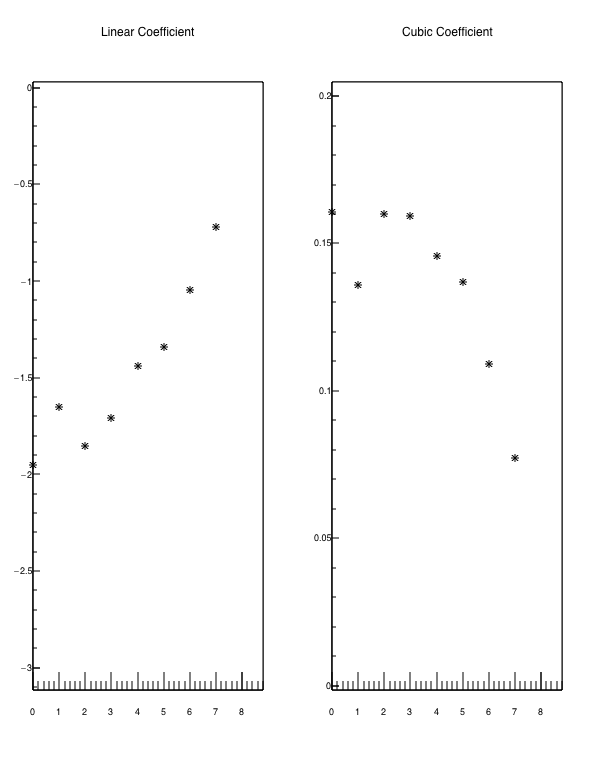
Figure 9 - linear (left) and cubic (right) fit parameters to the v1-versus-eta data, as a function of centrality. centID=0 are the most peripheral collisions (70-80%) and centID=8 are the most central (0-5%). The fit parameters for centID=8 are not shown, as the data were not stable so the fit was not stable.
It is worthwhile to point out that, while the v1 data in figures 1-8 give the impression of very little centrality dependence, when the curves are summarized by parameters as in figure 9, there is indeed a clear centrality dependence. The magnitude (note that the linear term is negative) of the linear and the cubic terms fall steadily and by twofold, as the centrality is changed.
Numerically....
Table 1 - Linear and cubic coefficients that parameterize the eta-dependence for v1 in the 9 centrality bins used. Two centrality bins (2 and especially 8) are outliers (see also figure 9), so I am changing them by hand. The value returned by the fit is shown in parentheses and crossed out; the value I will use is given first.
NB: these numbers are not going to be published, so I'm not going to spend a lot of time justifying my by-hand changes, or doing systematic studies. They are only weights to put into the EP finding algorithm. There are no wrong weights! "Better" weights give better resolution, that's all. But when things are resolution-corrected, any EP-finding algorithm should give the same result. (Just the errorbars will be different. My goal here is to maximize the resolution, hence minimizing errorbars on our statistics-challenged analyses.)
And.... how did it work out?
Well..... I had expected modest improvement across the board. What I found was very little change at all:
.png)
Figure 10 - EP[1] resolution from the BES-I (black circles) is compared with two weighting methods (discussed in the text) using the EPD in 2018 Au+Au 27 GeV running.
So, it seems that the two methods give essentially the same results. Not crazy. This is for events near the center of the TPC, where ring:eta is a fixed mapping. In future analyses, I will use the centrality- and eta-dependent v1 as the weights, as they should be more robust against fluctuations in the primary vertex position.
Table 1 - First-order event plane resolutions for various centrality classes. The second column indicates the values used in the polarization Nature paper in 2017. Third and fourth columns correspond to two different weighting schemes discussed in the text. Marginally-significant differences (anything higher than ~1%) highlighted in bold text.
It can be expected that v1-based weights are better, so the modest improvement for peripheral collisions makes sense. Why is the v1-based weighting method a little worse for the most central events? I don't know, but (1) the flow is small there; (2) v1-based weights don't have to be better; (3) the effect is so small that it may be nothing more than a fluctuation. So I'm not going to worry about it.
Update posted 24 Oct 2018
As discussed on the StEpdEpFinder page, one can turn on or turn off the eta-weights. Here are the correlations between East and West first-order angles, with eta-weights on and off: Clearly the weights can be very important!
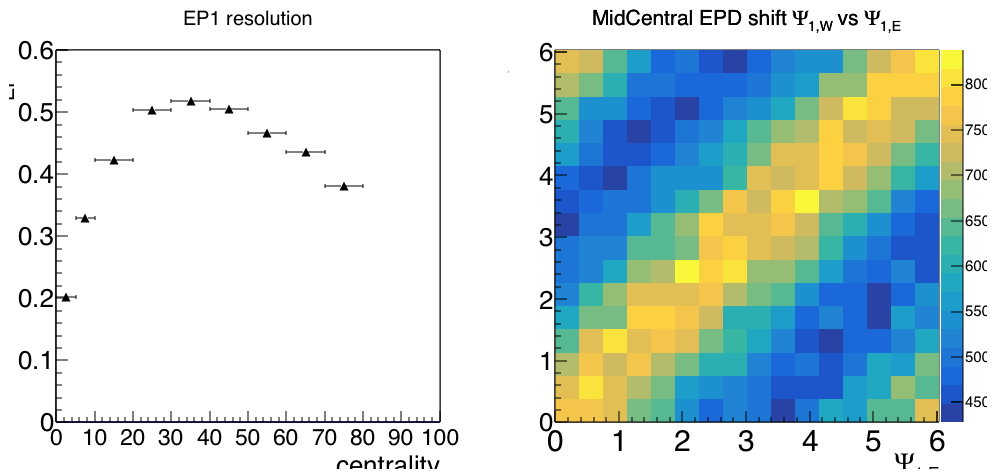
Figure 11 - Mid-central (centID=4-6, or 10-40% central) collisions, the correlation between East and West EPD event plane angles, fully corrected and Psi-shifted, when eta weights are ON.
.png)
Figure 12 - Mid-central (centID=4-6, or 10-40% central) collisions, the correlation between East and West EPD event plane angles, fully corrected and Psi-shifted, when eta weights are OFF.
Executive summary:
I have shown previously the importance of giving different EPD rings "weights," when finding the first-order event plane in Au+Au collisions at 27 GeV. As I said (as did Gang Wang), the weights should in principle depend on eta, not weight. A natural weighting would be the v1 signal itself (though it may not be the best, as net flux depends on eta, too, and could be part of the equation as well.)
Here, I find that weighting with centrality- and eta-dependent v1 gives basically the same result as weighting with the centrality-independent and ring-dependent values that were originally optimized for 10-40% centrality.
Going forward, it is probably best to switch to the v1(centrality,eta) weights, since they are more likely to be robust against primary vertex fluctuations, though this will need to be confirmed.
The directed flow depends on eta and on centrality. Capturing all of this dependence to generate weights is much easier if we fit the eta dependence, and then have the fit parameters depend on centrality bin. This turns out to be quite easy. Here are cubic ("pol3") fits to v1-versus-eta. The quadratic coefficient is always consistent with zero. The constant term is always a little bit negative (as I've mentioned before), but is insignificant here so I ignore it.
Except for the 0-5% bin, where the v1 determination doesn't converge well (I'm sure I could fix it if I put in the effort but not now), a cubic fit represents the data perfectly. Certainly good enough for our purposes.

.png)
.png)
.png)
.png)
.png)
.png)
.png)
Figures 1-8: Corrected v1 in eight centrality bins (0-5% has problems so not shown), with a cubic fit. Only the x and x3 terms are important.
Here are the fit parameters themselves, as a function of "centID". centID=0 means 70-80%. CentID=8 means 0-5%.

Figure 9 - linear (left) and cubic (right) fit parameters to the v1-versus-eta data, as a function of centrality. centID=0 are the most peripheral collisions (70-80%) and centID=8 are the most central (0-5%). The fit parameters for centID=8 are not shown, as the data were not stable so the fit was not stable.
It is worthwhile to point out that, while the v1 data in figures 1-8 give the impression of very little centrality dependence, when the curves are summarized by parameters as in figure 9, there is indeed a clear centrality dependence. The magnitude (note that the linear term is negative) of the linear and the cubic terms fall steadily and by twofold, as the centrality is changed.
Numerically....
| centID | % | linear coefficient | cubic coefficient |
|---|---|---|---|
| 0 | 70-80% | -1.950 | 0.1608 |
| 1 | 60-70% | -1.900 |
0.1600 ( |
| 2 | 50-60% | -1.850 | 0.1600 |
| 3 | 40-50% | -1.706 | 0.1595 |
| 4 | 30-40% | -1.438 | 0.1457 |
| 5 | 20-30% | -1.340 | 0.1369 |
| 6 | 10-20% | -1.045 | 0.1092 |
| 7 | 5-10% | -0.717 | 0.0772 |
| 8 | 0-5% | -0.700 ( |
0.0700 ( |
Table 1 - Linear and cubic coefficients that parameterize the eta-dependence for v1 in the 9 centrality bins used. Two centrality bins (2 and especially 8) are outliers (see also figure 9), so I am changing them by hand. The value returned by the fit is shown in parentheses and crossed out; the value I will use is given first.
NB: these numbers are not going to be published, so I'm not going to spend a lot of time justifying my by-hand changes, or doing systematic studies. They are only weights to put into the EP finding algorithm. There are no wrong weights! "Better" weights give better resolution, that's all. But when things are resolution-corrected, any EP-finding algorithm should give the same result. (Just the errorbars will be different. My goal here is to maximize the resolution, hence minimizing errorbars on our statistics-challenged analyses.)
And.... how did it work out?
Well..... I had expected modest improvement across the board. What I found was very little change at all:
.png)
Figure 10 - EP[1] resolution from the BES-I (black circles) is compared with two weighting methods (discussed in the text) using the EPD in 2018 Au+Au 27 GeV running.
So, it seems that the two methods give essentially the same results. Not crazy. This is for events near the center of the TPC, where ring:eta is a fixed mapping. In future analyses, I will use the centrality- and eta-dependent v1 as the weights, as they should be more robust against fluctuations in the primary vertex position.
| Cent | BES-I | EPD with RG16 Ring Weights | EPD with centrality and eta-dependent weights | eta-weighted / BES-1 (i.e. improvement factor) |
|---|---|---|---|---|
| 0-5% | 0.118 | 0.209 (6% higher) |
0.197 | 1.67 |
| 5-10% | 0.225 | 0.327 (3% higher) | 0.319 | 1.42 |
| 10-20% | 0.307 | 0.428 | 0.422 | 1.37 |
| 20-30% | 0.347 | 0.496 | 0.498 | 1.44 |
| 30-40% | 0.338 | 0.506 | 0.515 | 1.52 |
| 40-50% | 0.294 | 0.501 | 0.503 | 1.71 |
| 50-60% | 0.230 | 0.464 | 0.462 | 2.01 |
| 60-70% | 0.159 | 0.418 | 0.435 (4% higher) | 2.74 |
| 70-80% | 0.092 | 0.351 | 0.375 (6% higher) | 4.08 |
It can be expected that v1-based weights are better, so the modest improvement for peripheral collisions makes sense. Why is the v1-based weighting method a little worse for the most central events? I don't know, but (1) the flow is small there; (2) v1-based weights don't have to be better; (3) the effect is so small that it may be nothing more than a fluctuation. So I'm not going to worry about it.
Update posted 24 Oct 2018
As discussed on the StEpdEpFinder page, one can turn on or turn off the eta-weights. Here are the correlations between East and West first-order angles, with eta-weights on and off: Clearly the weights can be very important!

Figure 11 - Mid-central (centID=4-6, or 10-40% central) collisions, the correlation between East and West EPD event plane angles, fully corrected and Psi-shifted, when eta weights are ON.
.png)
Figure 12 - Mid-central (centID=4-6, or 10-40% central) collisions, the correlation between East and West EPD event plane angles, fully corrected and Psi-shifted, when eta weights are OFF.
»
- lisa's blog
- Login or register to post comments
