Phi-weighting and optimizing ring weights in Au+Au 27 GeV
Updated on Wed, 2018-06-13 20:16. Originally created by lisa on 2018-05-31 18:33.
Executive summary:
Note: this post has been updated to compare the optimized resolution to that from BES-I. Click here.
I have previously described a method of determining the "ring weights" Zr, that will provide the optimal EP resolution. (For a reminder of ring weight definition and how it is used to find event plane, see for example this post.) In my post, I performed the method for the 2nd-order event plane (EP[2]) for the isobar run. For isobar collisions at 200 GeV, I found that it was best if all rings were weighted more or less equally.
However, in my post from yesterday, I clearly showed that a ring-dependent weight must be used for the Au+Au data at 27 GeV. I explored a few examples by hand, but did not optimize according to the method mentioned above.
The main reason: the optimization method works if the particle azimuthal distribution is isotropic. In our case, mostly because of the bloody fixed-target holder, it is not. We remedy this with the "shifting method" which takes a non-flat EP distribution and flattens it. This is excellent, but it only works at the event-plane level, whereas to optimize ring weights, one wants isotropy already at the ring level. Here, I show how to achieve this, and that subsequent weight optimization allows us to extract important information from all rings.
Phi-weighting in the EPD
One way to isotropize is via the so-called "phi-weighting method." (Where an ADC value is measured instead of a track, this is sometimes (incorrectly) called "gain matching.") This is trivial to implement in a finite-element system like the EPD. And the first important result of this post is that phi-weighting at the tile level already flattens the EP at the event level; no further "shifting" is required. This is a non-trivial result.
What is the phi-weighting method?
The phi-weighting method assumes that all tiles in a given ring receive, averaged over events, the same particle flux; so long as the beam is on average along the beamline, this is surely true. A tile produces a signal assumed to be proportional to the flux in an event. Since the "tile signal" we use is the weight Wk that has a "MAX" associated with it, pure linearity certainly is not true; nevertheless, we push on...
Any anisotropy in the inclusive distribution (dW/dphi) is treated as a kind of "inefficiency," to be corrected with a phi-dependent (in our case, tile-dependent) factor bk:
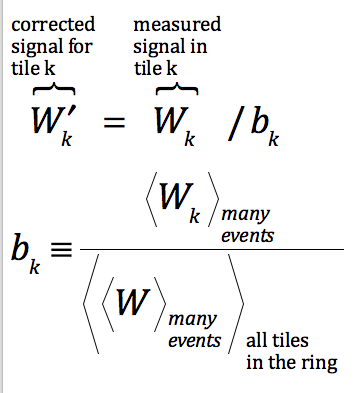
Now, the main source of anisotropy in our case is due to scattering in upstream material; far from an inefficiency, this material causes a multiplying effect-- we get too many particles! This corresponds to bk>1.0. In fact, we see from the math above, that the average bk in a ring must be unity. In principle, this could be a problem: just because tiles on the bottom part of ring 4 on the west side see too many particles and so must have their signals dampened (bk>1.0), there is no reason to think that tiles on the top of ring 4 are seeing too few particles. And yet the formalism described here will amplify their signal somewhat (bk<1.0). This "problem" should not be a big deal, in my opinion, unless the anisotropies are enormous. (And they are not. They are at the 8% level or less.)
EPD phi weights
Below, the phi-weights are shown in polar format. The coefficients bk are unity to within ~5%.
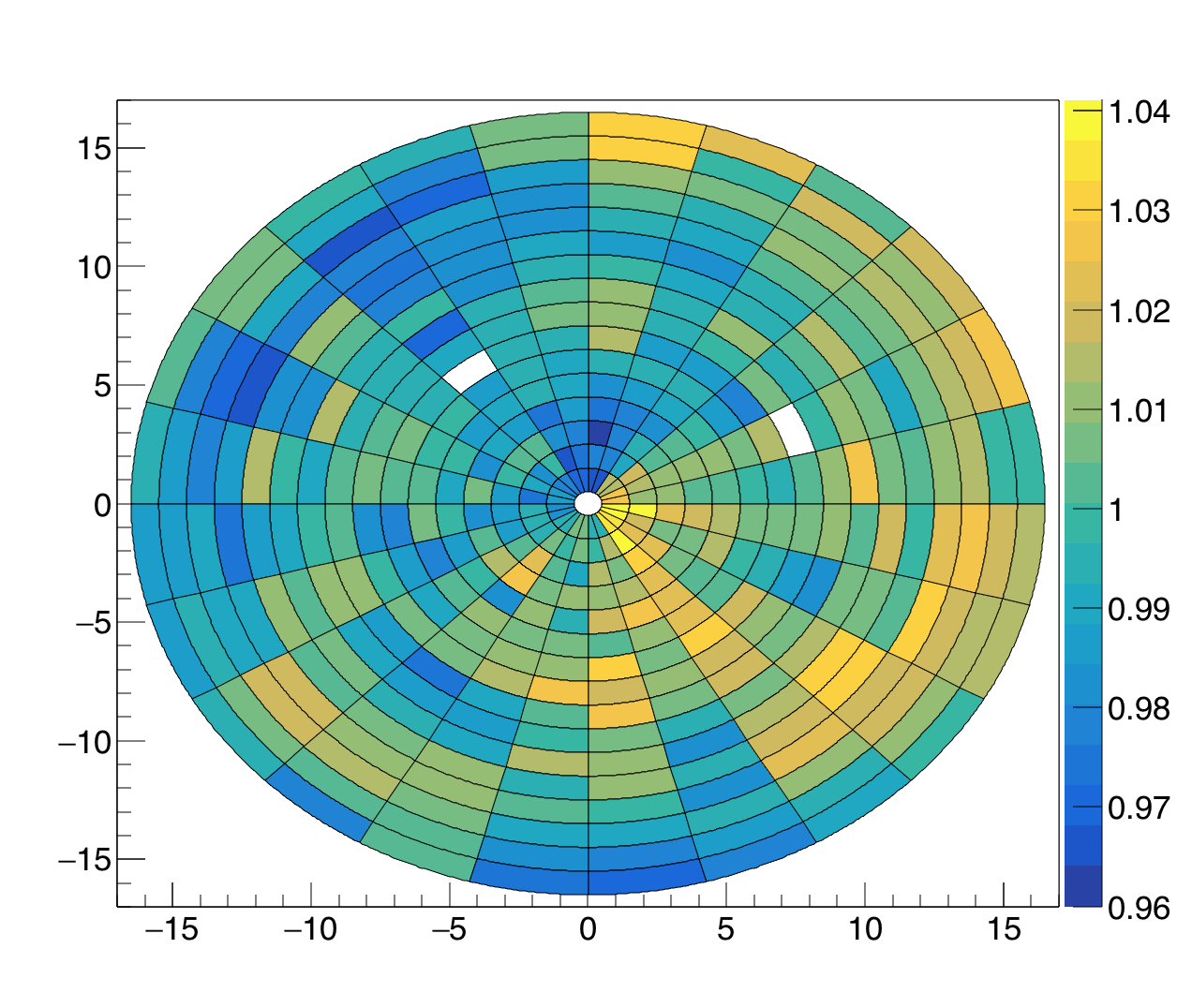
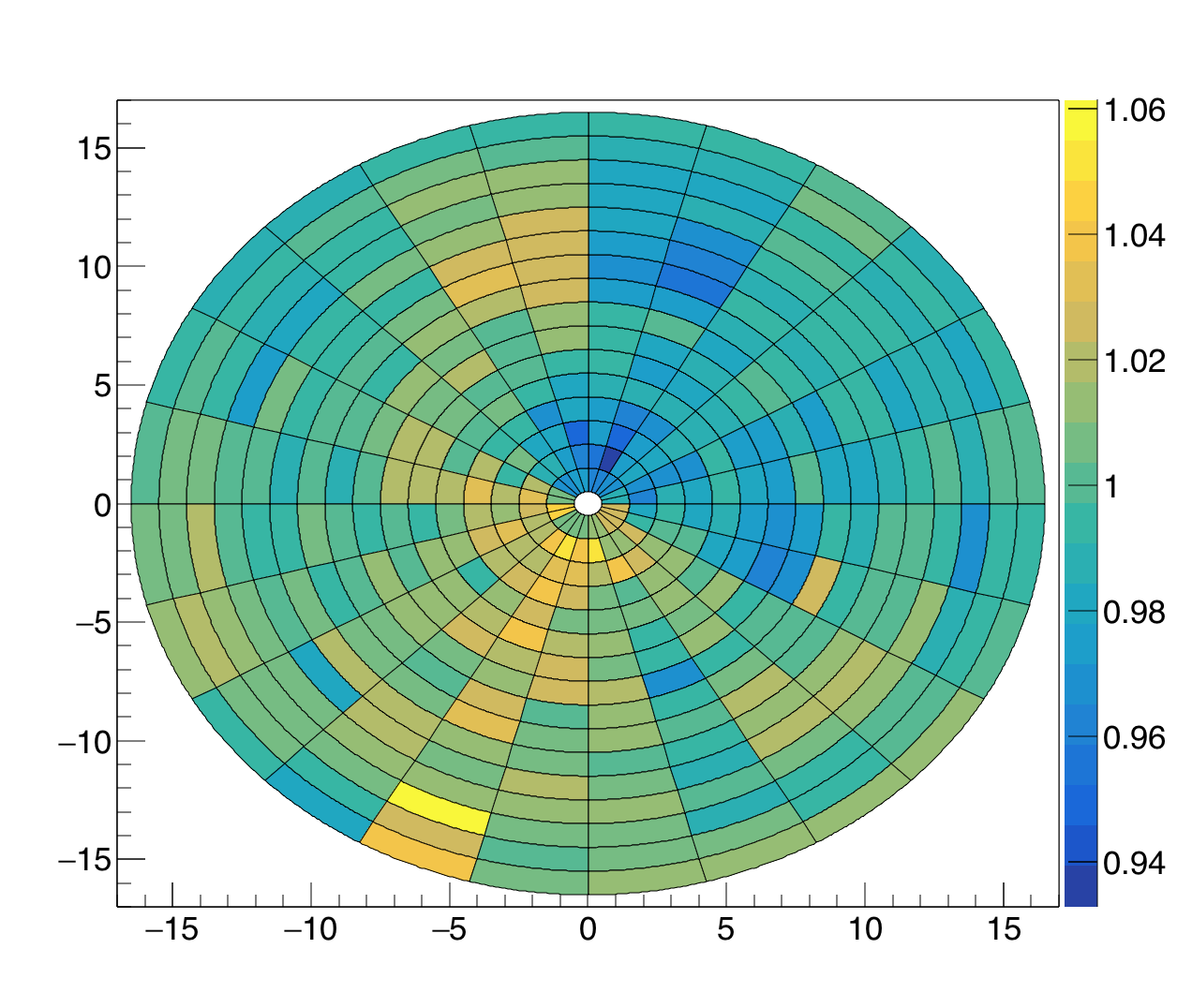
Figure 1 - Phi-weights for East (left) and West (right) EPD. On the East EPD, two tiles were around 0.92; I zoomed in the z-scale a bit, to center the color range and show a little detail.
Besides a random slighly hot or cold tile, one can see in rings 2-5 slightly higher signal toward the bottom (y<0) North (x<0) of the West EPD. As has been explained before, this is probably due to the fixed-target frame. Below I copy part of one slide from that post. There may be some excess yield in the South for the East EPD, as well, not noted previously. Tile-by-tile, none of these weights is larger than 8% away from unity.

Figure 2 - Azimuthal distributions of tile weights in the rings on the East (black) and West (red) sides. This is using nMIP as the weight, and is for the isobar run, but the point is that we see excess yield on the bottom of West rings 2-5. Taken from drupal.star.bnl.gov/STAR/blog/lisa/epd-sees-fixed-target-mount-2018-run
Effect on the Event Plane distribution:
We apply the phi-weights at the tile level prior to applying the "shift-correction" to the EP at the event level. This has advantages I will discuss below. It also has advantages of essentially making unnecessary the shift correction altogether! Below are plotted EP[1], EP[2] and EP[3] from both wheels. Red is after phi-weighting, and blue is after phi-weighting and then shifting. Both are flat to the few percent level.
.png)
.png)
.png)
Figure 3. First- (top row), second- (middle row) and third- (bottom row) order event planes for mid-central Au+Au collisions at 27 GeV, measured in the EPD. Left/Right column is East/West EPD. Red curves show the distribution after phi-weighting. Blue curves show after phi-weighting and then shifting.
Optimizing Ring Weights
As reported by ShinIchi and later by me, some EPD rings are more sensitive to EP[1] and should be "weighted" more than the others. I have previously described a method to find the optimum ring weights that maximizes the EP resolution. (In that study, I found that all rings should be weighted more or less equally for EP[2] in the 200 GeV isobar run.) While I didn't discuss it, that method implicitly assumes that the "event plane distribution for each ring individually" is flat. This cannot be (easily) done by shifting, but does happen perforce with the phi-weighting method. So, now that phi-weighting works, we can optimize ring weights.
I focus on midcentral (~10-40%) Au+Au collisions near the center (|Vz|<30 cm) of the TPC. For the raw tile weights, I use MAX=2.0.
I group the rings into ringgroups (RGs) consisting of 16, 8, 4, 2, 1 rings. The first case means just one ringgroup, so all rings are weighted precisely the same: this is the "standard Q-vector method." The last case means that each ring has its own weight. I group together all events in the 10-20%, 20-30%, and 30-40% classes.
Table 1 - Ring weights that maximize the EP[1] resolution for 10-40% central Au+Au events. In the second column, there is one ringgroup consisting of all 16 rings. In the final column, each ring is a ringgroup. The first RG has weight 100 by definition, since only relative weights matter.
Comments:
Implementation:
Using the RG16 weights to analyze the same 10-20%, 20-30%, 40-50% data as I have done previously (here and here), the results are below.
.png)
Figure 4 - First-order event plane study for mid-central collisions, when using the RG16 ring weights from Table 1. Pad 1: EP[1] resolution. (Note that only the 10-20%, 20-30% and 30-40% bins are studied, so all others are zero.) Pad 2: EP in East versus West, for flattened (shifted) event planes. Pads 3 and 4: Phi-weighted (red) and weighted-then-shifted (blue) EP resolution for East and West wheels, respectively. Pad 5: ignore. Pad 6: RefMult distribution. We are using the third, fourth and fifth bins from the right.
The result: We have seen REP(1) > 0.5 for the first time. Below I tabulate the 1st-order EP resolution for the various approaches using the EPD, as well as the resolution achieved in BES-I (used in the v1 analysis (and this), Lambda polarization, etc.)
Table 2 - EP[1] resolution (calculated the "correct way," by the way, not simply sqrt(2*<cos(DeltaPhi)>)) three centrality bins. Column 2: weighting all tiles equally. Column 3: what was used in BES-I analyses, using the BBC. Column 4: Only using rings 1-2 (innermost rings) and ignoring all others. Column 5: using optimized ring weights (see Table 1) for all 16 rings. Column 6: The improvement so far (ratio of columns 5 and 3).
While the "naive" (non-weighting) Q-vector method gives 3x worse resolution than BES-I, the optimized method gives us a 40-50% improvement over BES. In terms of signal significance for v1, polarization, etc, this is equivalent to a factor ~2 in statistics.
Ignoring the outer padrows altogether reduces the resolution by ~15% (compare columns 4 and 5), which is not insignificant.
Not bad, but I'd like to do better. Who can be clever enough to get us to 70% improvement over BES-I?
Update 6 June 2018 - comparing optimized RG16 to BES-I for all centralities:
Table 3 - First-order EP resolution from BES-I (e.g. the analysis used in the Nature paper on polarization) is compared to the resolution obtained from the EPD using ring weights in the rightmost column of table 1.
Interesting that the data suggest that the improvement is bigger for more peripheral events. This might be due to simply a larger acceptance and hence less statistical fluctuations for low flux.

Figure 5 - First-order EP resolution as a function of collision centrality, for 27 GeV Au+Au collisions. Numbers tabulated in table 3.
I emphasize that this is very nice. While there were sometimes expectations of two-fold improvement in EP resolution, I remind those who were there, that I suggested to expect only 50% improvement, and this is indeed what we see for the midcentral collisions. (Admission: it was a guess.) However, for the more peripheral events-- where effects like polarization might be more important-- the improvement is significantly better, indeed reaching a two-fold improvement. As a matter of fact, the cross-section-weighted average of the "improvement factors" in the right-most column of table 3 is....... 2.01.
This is important. In the BES-I polarization paper, we had only three centrality bins with resolution above 0.3. In the new data, all except 0-5% are above 0.3. This may allow us to do a lot more.
- Ring-by-ring azimuthal anisotropies in the EPD are at the level of ~8% or less.
- Phi-weighting can be used to remove these anisotropies on average (perforce). Less trivially, it also renders unnecessary EP "shifting" corrections at the event level.
- This enforced ring-by-ring isotropization makes it possible to tune the event-plane-finding algorithm to maximize the EP resolution.
- After such optimization, the EP resolution is improved by ~45% relative to BES-I values.
Note: this post has been updated to compare the optimized resolution to that from BES-I. Click here.
I have previously described a method of determining the "ring weights" Zr, that will provide the optimal EP resolution. (For a reminder of ring weight definition and how it is used to find event plane, see for example this post.) In my post, I performed the method for the 2nd-order event plane (EP[2]) for the isobar run. For isobar collisions at 200 GeV, I found that it was best if all rings were weighted more or less equally.
However, in my post from yesterday, I clearly showed that a ring-dependent weight must be used for the Au+Au data at 27 GeV. I explored a few examples by hand, but did not optimize according to the method mentioned above.
The main reason: the optimization method works if the particle azimuthal distribution is isotropic. In our case, mostly because of the bloody fixed-target holder, it is not. We remedy this with the "shifting method" which takes a non-flat EP distribution and flattens it. This is excellent, but it only works at the event-plane level, whereas to optimize ring weights, one wants isotropy already at the ring level. Here, I show how to achieve this, and that subsequent weight optimization allows us to extract important information from all rings.
Phi-weighting in the EPD
One way to isotropize is via the so-called "phi-weighting method." (Where an ADC value is measured instead of a track, this is sometimes (incorrectly) called "gain matching.") This is trivial to implement in a finite-element system like the EPD. And the first important result of this post is that phi-weighting at the tile level already flattens the EP at the event level; no further "shifting" is required. This is a non-trivial result.
What is the phi-weighting method?
The phi-weighting method assumes that all tiles in a given ring receive, averaged over events, the same particle flux; so long as the beam is on average along the beamline, this is surely true. A tile produces a signal assumed to be proportional to the flux in an event. Since the "tile signal" we use is the weight Wk that has a "MAX" associated with it, pure linearity certainly is not true; nevertheless, we push on...
Any anisotropy in the inclusive distribution (dW/dphi) is treated as a kind of "inefficiency," to be corrected with a phi-dependent (in our case, tile-dependent) factor bk:

Now, the main source of anisotropy in our case is due to scattering in upstream material; far from an inefficiency, this material causes a multiplying effect-- we get too many particles! This corresponds to bk>1.0. In fact, we see from the math above, that the average bk in a ring must be unity. In principle, this could be a problem: just because tiles on the bottom part of ring 4 on the west side see too many particles and so must have their signals dampened (bk>1.0), there is no reason to think that tiles on the top of ring 4 are seeing too few particles. And yet the formalism described here will amplify their signal somewhat (bk<1.0). This "problem" should not be a big deal, in my opinion, unless the anisotropies are enormous. (And they are not. They are at the 8% level or less.)
EPD phi weights
Below, the phi-weights are shown in polar format. The coefficients bk are unity to within ~5%.


Figure 1 - Phi-weights for East (left) and West (right) EPD. On the East EPD, two tiles were around 0.92; I zoomed in the z-scale a bit, to center the color range and show a little detail.
Besides a random slighly hot or cold tile, one can see in rings 2-5 slightly higher signal toward the bottom (y<0) North (x<0) of the West EPD. As has been explained before, this is probably due to the fixed-target frame. Below I copy part of one slide from that post. There may be some excess yield in the South for the East EPD, as well, not noted previously. Tile-by-tile, none of these weights is larger than 8% away from unity.

Figure 2 - Azimuthal distributions of tile weights in the rings on the East (black) and West (red) sides. This is using nMIP as the weight, and is for the isobar run, but the point is that we see excess yield on the bottom of West rings 2-5. Taken from drupal.star.bnl.gov/STAR/blog/lisa/epd-sees-fixed-target-mount-2018-run
Effect on the Event Plane distribution:
We apply the phi-weights at the tile level prior to applying the "shift-correction" to the EP at the event level. This has advantages I will discuss below. It also has advantages of essentially making unnecessary the shift correction altogether! Below are plotted EP[1], EP[2] and EP[3] from both wheels. Red is after phi-weighting, and blue is after phi-weighting and then shifting. Both are flat to the few percent level.
.png)
.png)
.png)
Figure 3. First- (top row), second- (middle row) and third- (bottom row) order event planes for mid-central Au+Au collisions at 27 GeV, measured in the EPD. Left/Right column is East/West EPD. Red curves show the distribution after phi-weighting. Blue curves show after phi-weighting and then shifting.
Optimizing Ring Weights
As reported by ShinIchi and later by me, some EPD rings are more sensitive to EP[1] and should be "weighted" more than the others. I have previously described a method to find the optimum ring weights that maximizes the EP resolution. (In that study, I found that all rings should be weighted more or less equally for EP[2] in the 200 GeV isobar run.) While I didn't discuss it, that method implicitly assumes that the "event plane distribution for each ring individually" is flat. This cannot be (easily) done by shifting, but does happen perforce with the phi-weighting method. So, now that phi-weighting works, we can optimize ring weights.
I focus on midcentral (~10-40%) Au+Au collisions near the center (|Vz|<30 cm) of the TPC. For the raw tile weights, I use MAX=2.0.
I group the rings into ringgroups (RGs) consisting of 16, 8, 4, 2, 1 rings. The first case means just one ringgroup, so all rings are weighted precisely the same: this is the "standard Q-vector method." The last case means that each ring has its own weight. I group together all events in the 10-20%, 20-30%, and 30-40% classes.
| RG | #RG=1 | #RG=2 | #RG=4 | #RG=8 | #RG=16 |
|---|---|---|---|---|---|
| 1 | 100 | 100 | 100 | 100 | 100 |
| 2 | -67 | -7 | 48 | 68 | |
| 3 | -30 | 3 | 44 | ||
| 4 | -26 | -18 | 31 | ||
| 5 | -12 | 3 | |||
| 6 | -20 | -6 | |||
| 7 | -26 | -17 | |||
| 8 | -14 | -16 | |||
| 9 | -2 | ||||
| 10 | -17 | ||||
| 11 | -15 | ||||
| 12 | -18 | ||||
| 13 | -14 | ||||
| 14 | -21 | ||||
| 15 | -12 | ||||
| 16 | -12 | ||||
| <cos(DeltaPsi[1])> | 0.0083 | 0.0576 | 0.1063 | 0.1215 | 0.1284 |
| REP(1) | 0.1283 | 0.3332 | 0.4455 | 0.4739 | 0.4861 |
Comments:
- As noted before, the flow/anti-flow pattern demands negative weights for the outer rings.
- Optimizing ring weights nearly quadruples the EP[1] resolution for Au+Au collisions at 27 GeV, as compared to naively weighting all tiles equally. This is in stark contrast to the EP[2] in the isobar run, where it had almost zero effect.
- One wants to "coarse grain" things a bit-- i.e. I would imagine that the "-2" weight for RG9 in the final column is a fluctuation. However, the large trends are clear. It is clear that the inner rings are much more important than the outer ones, at this energy. Keep in mind that on top of these ring weights is the integrated flux (simply "the average particle yield per event"), which is larger for the inner rings.
Implementation:
Using the RG16 weights to analyze the same 10-20%, 20-30%, 40-50% data as I have done previously (here and here), the results are below.
.png)
Figure 4 - First-order event plane study for mid-central collisions, when using the RG16 ring weights from Table 1. Pad 1: EP[1] resolution. (Note that only the 10-20%, 20-30% and 30-40% bins are studied, so all others are zero.) Pad 2: EP in East versus West, for flattened (shifted) event planes. Pads 3 and 4: Phi-weighted (red) and weighted-then-shifted (blue) EP resolution for East and West wheels, respectively. Pad 5: ignore. Pad 6: RefMult distribution. We are using the third, fourth and fifth bins from the right.
The result: We have seen REP(1) > 0.5 for the first time. Below I tabulate the 1st-order EP resolution for the various approaches using the EPD, as well as the resolution achieved in BES-I (used in the v1 analysis (and this), Lambda polarization, etc.)
| Centrality | naive | BES-I | Only R1-2 | 16 weights optimized | optimized / BES-I |
|---|---|---|---|---|---|
| 10-20% | 0.091 | 0.307 | 0.345 | 0.429 | 1.40 |
| 20-30% | 0.153 | 0.347 | 0.438 | 0.497 | 1.43 |
| 30-40% | 0.097 | 0.338 | 0.448 | 0.505 | 1.49 |
Table 2 - EP[1] resolution (calculated the "correct way," by the way, not simply sqrt(2*<cos(DeltaPhi)>)) three centrality bins. Column 2: weighting all tiles equally. Column 3: what was used in BES-I analyses, using the BBC. Column 4: Only using rings 1-2 (innermost rings) and ignoring all others. Column 5: using optimized ring weights (see Table 1) for all 16 rings. Column 6: The improvement so far (ratio of columns 5 and 3).
While the "naive" (non-weighting) Q-vector method gives 3x worse resolution than BES-I, the optimized method gives us a 40-50% improvement over BES. In terms of signal significance for v1, polarization, etc, this is equivalent to a factor ~2 in statistics.
Ignoring the outer padrows altogether reduces the resolution by ~15% (compare columns 4 and 5), which is not insignificant.
Not bad, but I'd like to do better. Who can be clever enough to get us to 70% improvement over BES-I?
Update 6 June 2018 - comparing optimized RG16 to BES-I for all centralities:
| Cent | BES-I | Optimized RG16 | Ratio |
|---|---|---|---|
| 0-5% | 0.118 | 0.209 | 1.77 |
| 5-10% | 0.225 | 0.327 | 1.45 |
| 10-20% | 0.307 | 0.428 | 1.39 |
| 20-30% | 0.347 | 0.496 | 1.43 |
| 30-40% | 0.338 | 0.506 | 1.50 |
| 40-50% | 0.294 | 0.501 | 1.70 |
| 50-60% | 0.230 | 0.464 | 2.02 |
| 60-70% | 0.159 | 0.418 | 2.62 |
| 70-80% | 0.092 | 0.351 | 3.82 |
Interesting that the data suggest that the improvement is bigger for more peripheral events. This might be due to simply a larger acceptance and hence less statistical fluctuations for low flux.

Figure 5 - First-order EP resolution as a function of collision centrality, for 27 GeV Au+Au collisions. Numbers tabulated in table 3.
I emphasize that this is very nice. While there were sometimes expectations of two-fold improvement in EP resolution, I remind those who were there, that I suggested to expect only 50% improvement, and this is indeed what we see for the midcentral collisions. (Admission: it was a guess.) However, for the more peripheral events-- where effects like polarization might be more important-- the improvement is significantly better, indeed reaching a two-fold improvement. As a matter of fact, the cross-section-weighted average of the "improvement factors" in the right-most column of table 3 is....... 2.01.
This is important. In the BES-I polarization paper, we had only three centrality bins with resolution above 0.3. In the new data, all except 0-5% are above 0.3. This may allow us to do a lot more.
»
- lisa's blog
- Login or register to post comments
