Ring weights for estimating global quantities with linear sums
Updated on Thu, 2020-03-26 09:52. Originally created by lisa on 2020-03-24 18:39.
I use UrQMD calculations for Au+Au collisions at 19.6 GeV. In a model, we might like to cut on the impact parameter, b. In data analysis, we might like to cut on the midrapidity multiplicity. My goal is to fashion a simple quantity from EPD ring data, that correlates tightly with one of these quantities. In their paper Chatterjee et al (arxiv.org/abs/1910.08004) show that simply using the number of tracks within the EPD eta range, gives a rather poor correlation to centrality, so would not be useful for their physics analysis.
However, they simply add all the rings together. As we know, at BES energies, as the collision becomes more central, some rings (e.g. inner) get LESS flux and others (e.g. outer) get MORE. So, there is information which these guys are throwing away.
One can try to exploit all possible information encoded in the data, to produce a better centrality estimator. Neural nets, machine learning, etc. I will do something much simpler-- simply a linear weighted sum of the contents of the 16 rings. (I will add East and West EPDs together, so we are only talking about 16 numbers.) What's cool is that there is no "learning" or "fitting" or anything-- the problem has a simple analytic solution that amounts to inverting a 16x16 real symmetric matrix.
Rosi has been looking at how various quantities, including individual rings and total multiplicity, correspond to impact parameter on her page: drupal.star.bnl.gov/STAR/blog/rjreed/centrality-epd-take-2
Si is the signal associated with tile i, and Cr is the contribution of ring r, found by summing the truncated-nMIP from all tiles in that ring. Both East and West are added. These quantities are defined as follows:
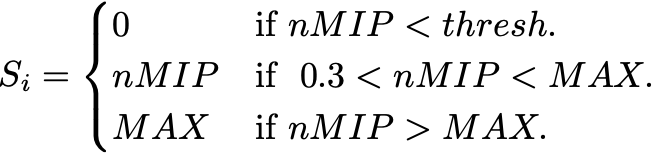
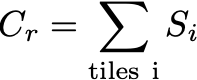
Our observable X is simply a weighted sum of the ring contents:
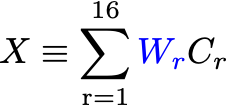
Our goal is to find the ring weights, Wr, that maximize the correlation between X and our global quantity of interest (impact parameter, TPC refMult, whatever).
To find the best weights, we minimize the squared residual
.png)
Where Gj is the value of the global quantity of interest in event j.
But we don't need to do some Minuit-driven minimization, or any learning or anything. At the minimum,
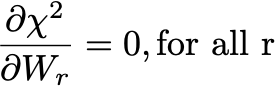
and it can be shown that they satisfy the 16 linear equations:
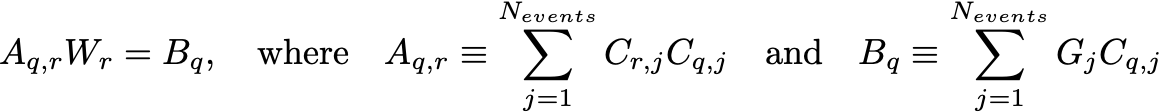
Since A is a symmetric, real 16x16 matrix, it is extremely easy and fast to invert, finding the unique best weights Wr.
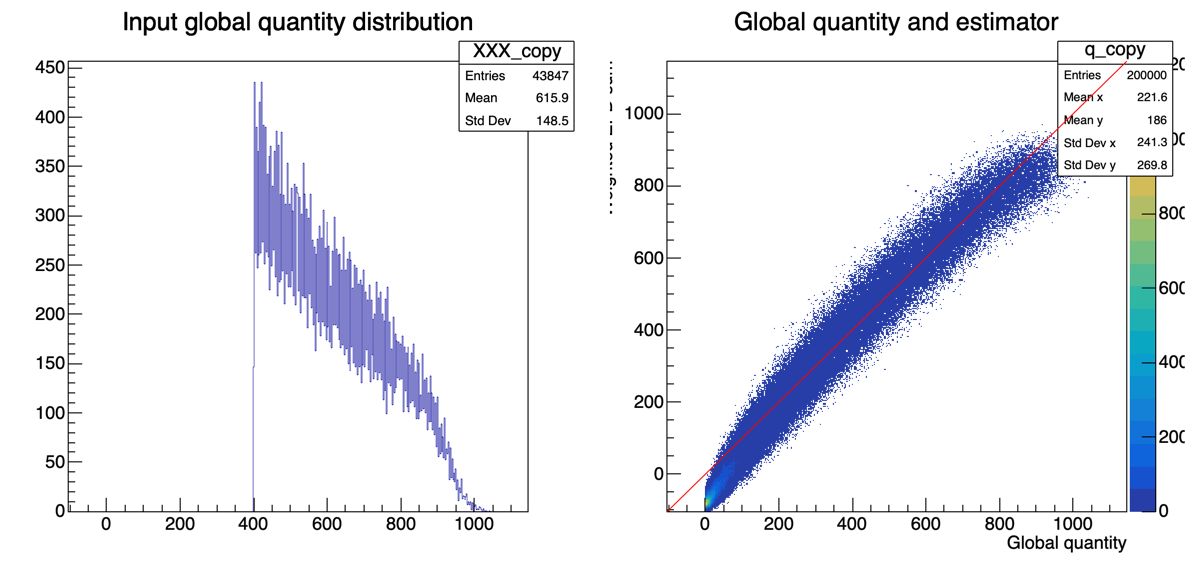
If we use the TPC charged particle multiplicity (|eta|<1) as the global quantity of interest, then
We may very well want to neglect the very peripheral collisions in our weighting. This is legitimate, as they might be uninteresting for us, and they are numerous. Here is what happens if we focus on events with refMult>400:
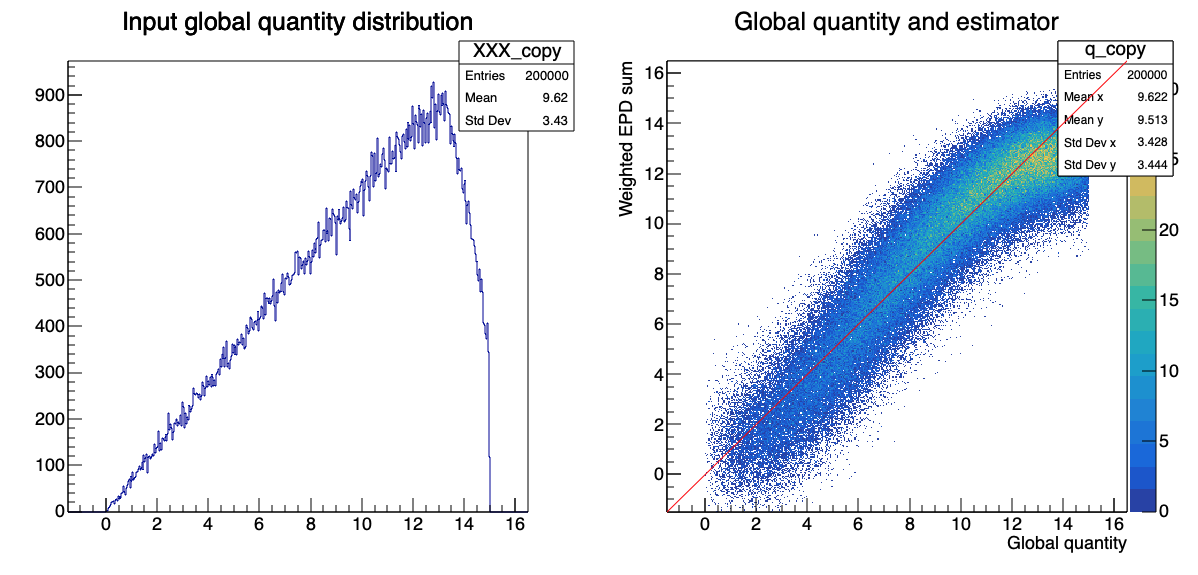
If we use the impact parameter as the global quantity of interest:
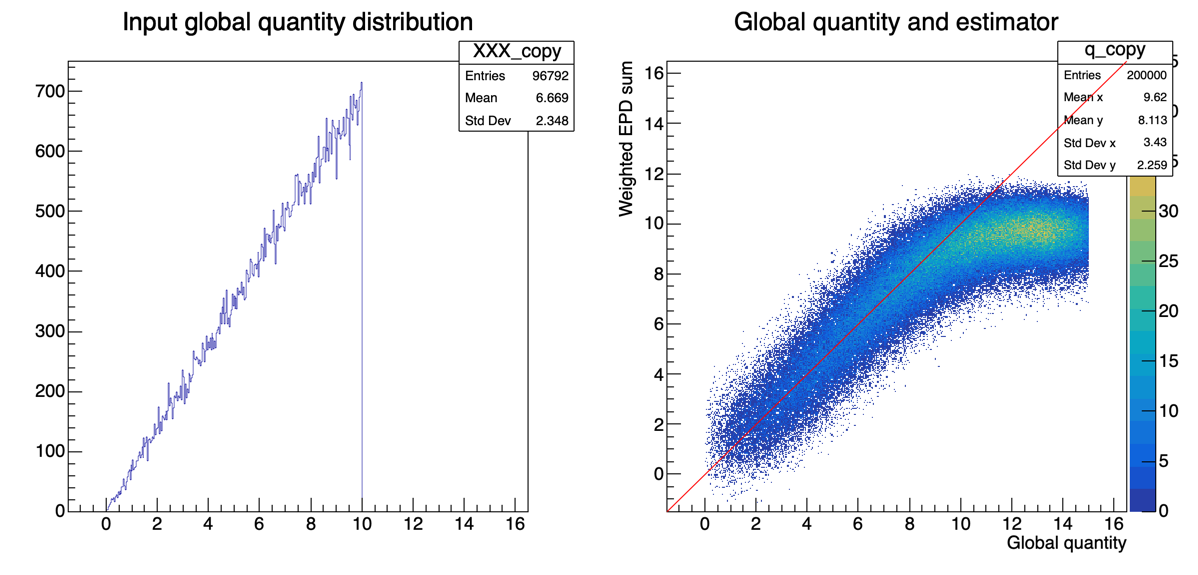
As above, we may want to neglect the most peripheral collisions, as they might be uninteresting for us, and skew our weights. Here is for b<10 fm.
While fancier techniques (nonlinear maps, learning, fitting) may yield slightly better results, this is already quite good and easy. Note that the weights have meaningful sign: as we said, inner and outer rings act oppositely, when the centrality is changed.
The macro for getting the weights is attached to the bottom of the page. Note it assumes that you have made an ntuple with 18 rows. 16 for the ring values (Cr above), then one for RefMult and one for impact parameter.
Overview:
My goal is to use EPD data to estimate a global quantity. This could be an event plane, as I've done often in the past. Here, I will focus on centrality.I use UrQMD calculations for Au+Au collisions at 19.6 GeV. In a model, we might like to cut on the impact parameter, b. In data analysis, we might like to cut on the midrapidity multiplicity. My goal is to fashion a simple quantity from EPD ring data, that correlates tightly with one of these quantities. In their paper Chatterjee et al (arxiv.org/abs/1910.08004) show that simply using the number of tracks within the EPD eta range, gives a rather poor correlation to centrality, so would not be useful for their physics analysis.
However, they simply add all the rings together. As we know, at BES energies, as the collision becomes more central, some rings (e.g. inner) get LESS flux and others (e.g. outer) get MORE. So, there is information which these guys are throwing away.
One can try to exploit all possible information encoded in the data, to produce a better centrality estimator. Neural nets, machine learning, etc. I will do something much simpler-- simply a linear weighted sum of the contents of the 16 rings. (I will add East and West EPDs together, so we are only talking about 16 numbers.) What's cool is that there is no "learning" or "fitting" or anything-- the problem has a simple analytic solution that amounts to inverting a 16x16 real symmetric matrix.
Rosi has been looking at how various quantities, including individual rings and total multiplicity, correspond to impact parameter on her page: drupal.star.bnl.gov/STAR/blog/rjreed/centrality-epd-take-2
The observable:
In every event, the EPD produces 16 numbers: the "contents" of the 16 rings. I will use the sum of the truncated-nMIP from all tiles in the ring.Si is the signal associated with tile i, and Cr is the contribution of ring r, found by summing the truncated-nMIP from all tiles in that ring. Both East and West are added. These quantities are defined as follows:
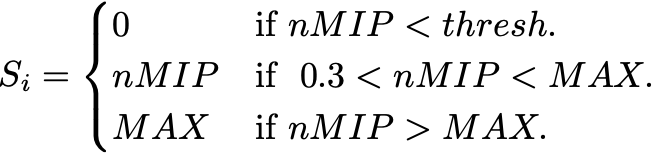
Our observable X is simply a weighted sum of the ring contents:
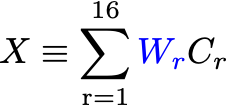
Our goal is to find the ring weights, Wr, that maximize the correlation between X and our global quantity of interest (impact parameter, TPC refMult, whatever).
Finding the weights:
To find the best weights, we minimize the squared residual
.png)
Where Gj is the value of the global quantity of interest in event j.
But we don't need to do some Minuit-driven minimization, or any learning or anything. At the minimum,
and it can be shown that they satisfy the 16 linear equations:
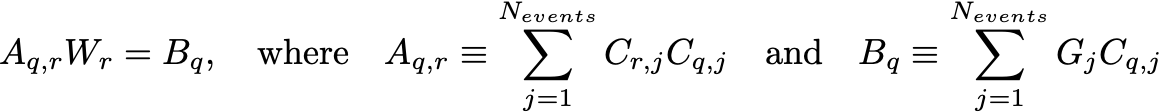
Since A is a symmetric, real 16x16 matrix, it is extremely easy and fast to invert, finding the unique best weights Wr.
Results:
In the present analysis, I used MAX=2.0 and thresh=0.0. (In data, there is electronic noise, so normally people use thresh=0.2 or 0.3. But there is little true signal below 0.2, so it's fine to use 0.0 here.)If we use the TPC charged particle multiplicity (|eta|<1) as the global quantity of interest, then
ring weight
1 -0.308569
2 -1.59856
3 -1.11792
4 -0.485728
5 0.078737
6 0.604919
7 1.06758
8 1.36972
9 1.70278
10 1.99164
11 2.09085
12 2.31006
13 2.39085
14 2.5433
15 2.62684
16 2.77495
We may very well want to neglect the very peripheral collisions in our weighting. This is legitimate, as they might be uninteresting for us, and they are numerous. Here is what happens if we focus on events with refMult>400:
ring weight
1 -2.21991
2 -0.519672
3 -0.268216
4 0.26761
5 0.61744
6 0.981569
7 1.21238
8 1.43501
9 1.69529
10 1.85845
11 1.99035
12 2.03898
13 2.15267
14 2.36434
15 2.26262
16 2.41752

If we use the impact parameter as the global quantity of interest:
ring weight
1 0.321766
2 -0.0367021
3 -0.0294183
4 -0.0233452
5 -0.0155745
6 -0.0104552
7 -0.00570113
8 -0.00269207
9 -0.00176239
10 0.00255536
11 -0.00136428
12 0.0021822
13 0.00384546
14 0.00157523
15 0.00514248
16 0.00521579

As above, we may want to neglect the most peripheral collisions, as they might be uninteresting for us, and skew our weights. Here is for b<10 fm.
ring weight
1 0.24169
2 0.0329237
3 0.0235763
4 0.0151417
5 0.0096042
6 0.00305559
7 -0.00285034
8 -0.0026057
9 -0.0077434
10 -0.00913805
11 -0.0107693
12 -0.0115195
13 -0.0100566
14 -0.0121149
15 -0.012695
16 -0.0134135

While fancier techniques (nonlinear maps, learning, fitting) may yield slightly better results, this is already quite good and easy. Note that the weights have meaningful sign: as we said, inner and outer rings act oppositely, when the centrality is changed.
The macro for getting the weights is attached to the bottom of the page. Note it assumes that you have made an ntuple with 18 rows. 16 for the ring values (Cr above), then one for RefMult and one for impact parameter.
»
- lisa's blog
- Login or register to post comments

.png)