In order to verify the tile mapping between "TUFF space" and "StEvent space", we have been setting Vped to different values  (in "TUFF space") and seeing the results in StEvent.  See this link for an overview:  drupal.star.bnl.gov/STAR/blog/lisa/checking-mapping-all-way-tuff-box-stevent-and-mudst

This has already identified mapping errors, which we have corrected.  See this page:  drupal.star.bnl.gov/STAR/blog/rjreed/testing-epd-mapping-part-1

Rosi has produced very nice pattern files, but they do not absolutely resolve all ambiguity.  I.e. two tiles could be swapped, and in principle, Rosi's patterns would not reveal it.  In principle, one could turn on each of our 744 tiles one at a time, but this is entirely impractical.  Setting the Vped takes minutes and each run takes minutes and then the transfer and offline takes minutes.  Gerard pointed out that one does not need 744 runs.  While I disagreed with him at first, it occurs to me that he was right (as usual.....)

Here I present a set of just seven patterns that, if there is agreement between TUFF and StEvent spaces, guarantees that the mapping is 100% correct.

These pictures are made with a root macro which you can find attached to the bottom of the page (or else click here).  Naturally, you can use this macro to generate the Vped pattern file itself.


I am using the scheme that there are three Vped levels that we can set and discriminate offline.  In order to keep consistent with our previous plots, Level 0 is blue, Level 1 is green, Level 2 is red.

---

Pattern 1: - Disambiguate East and West
East at 1, West at 2



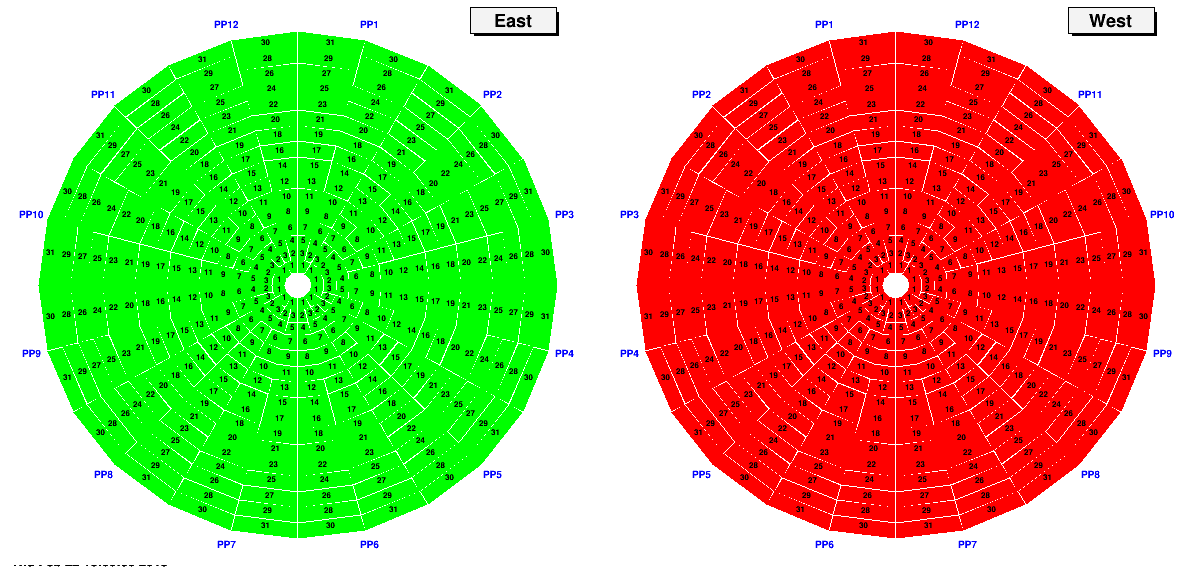
This will identify whether anybody is entirely missing.  Also, whether there is any accidental swapping of East to West.
If this test is passed, then one can run simultaneous tests on East and West.

---

Pattern 2 - Break each wheel into thirds
PP01-04 at level 0
PP05-08 at level 1
PP09-12 at level 2



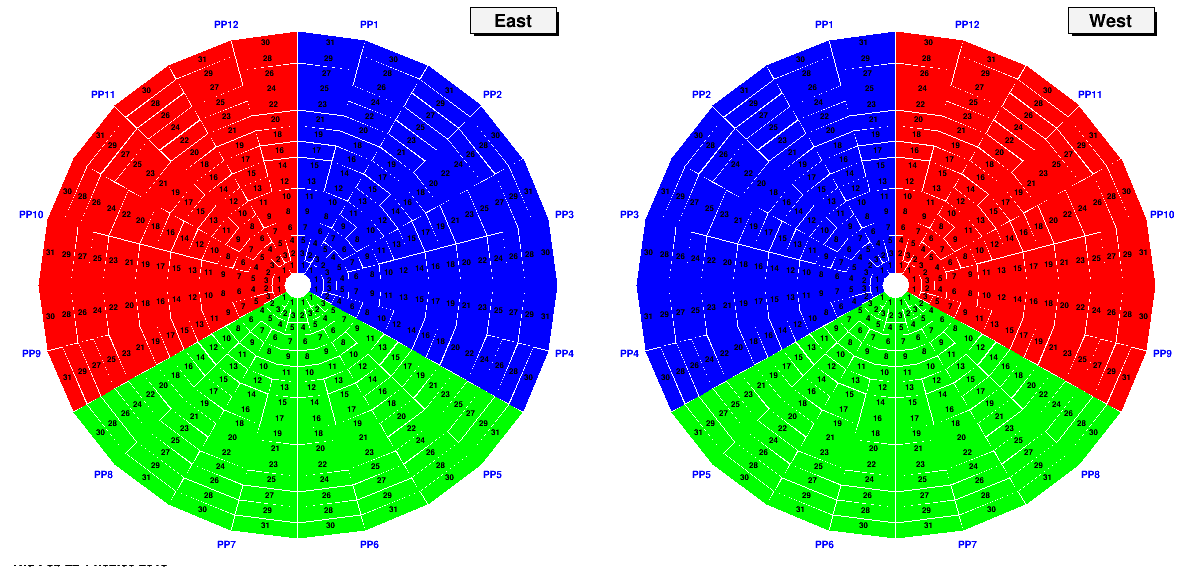
If this test is passed, then one only needs to look for accidental swaps within a third-wheel.

---

Pattern 3 - Break each third-of-a-wheel into thirds
The "quantum" of color is now the SECTOR, rather than supersector.




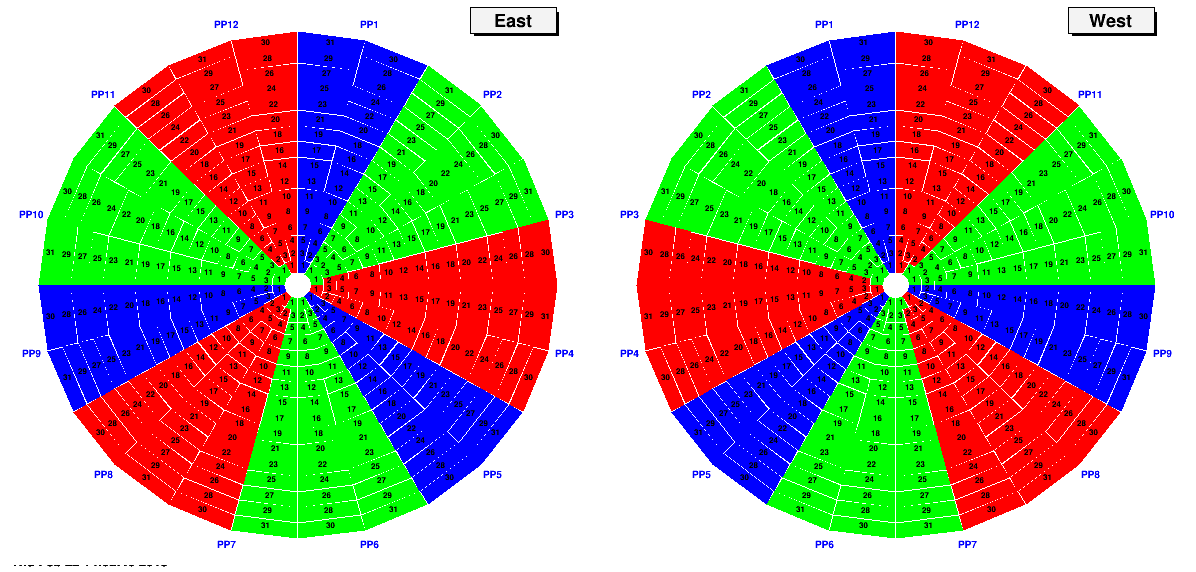
If this test is passed, then only need look for accidental swaps within each ninth-of-a-wheel

And each of these groups has at most three sectors.

---

Pattern 4 - Breaking each ninth-of-a-wheel into thirds



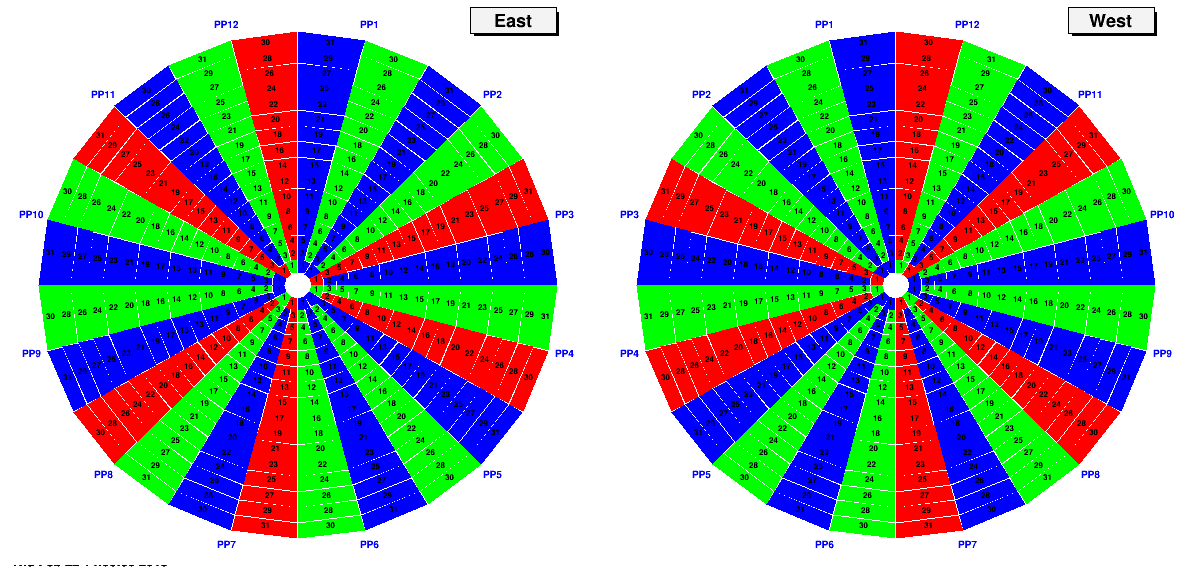
If the test has satisfied pattern 4, then we know that any accidental swap is happening entirely within a sector (remember, sector is half of a supersector, i.e. the odds or the evens)

---

Pattern 5 - Breaking each sector into three groups of tiles
For the first time, we are looking for swap structure within a sector
Tiles 1-11 at level 1
Tiles 12-21 at level 2
Tiles 22-31 at level 3



If we pass this test, then we only need to look for accidental swaps within a group of 5 or 6 tiles.  This takes only two more steps, which follow:

---

Pattern 6 - looking within tile groups



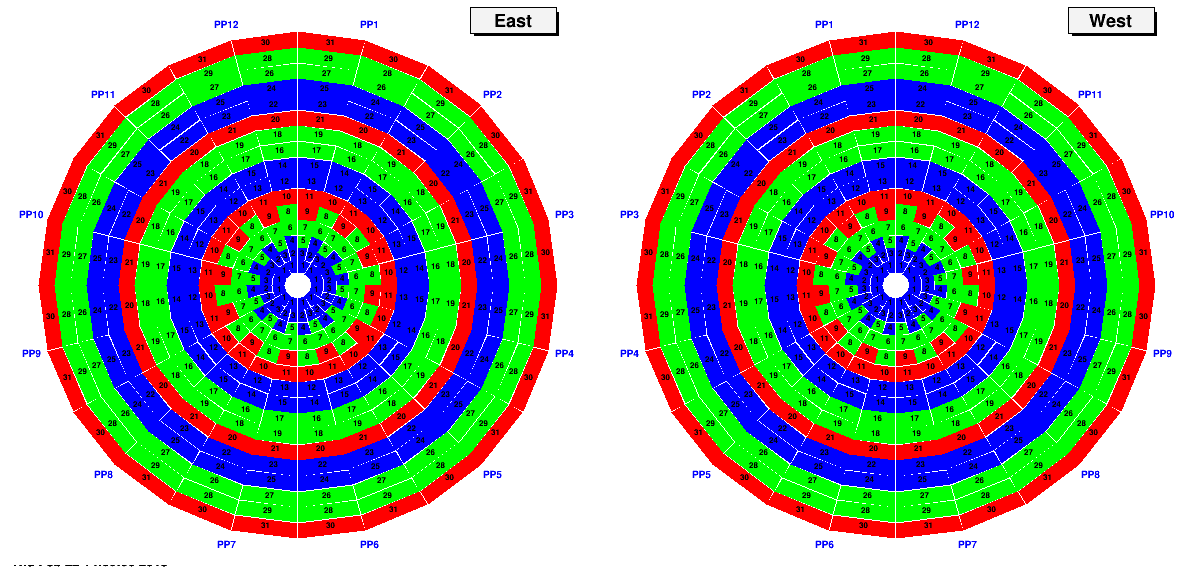
If we pass this test, then for some of the tiles (TT21,31,10,20,30) there is zero ambiguity.  They are definitely mapped correctly.

There are still pairs which must be discriminated: (1,3), (5,7), (9,11), (13,15), (17,19), (23,25), (27,29), (2,4), (6,8), (12,14), (16,18), (22,24), (26,28).  This is done on the next and final step:

---

Pattern 7 - Final resolution

---

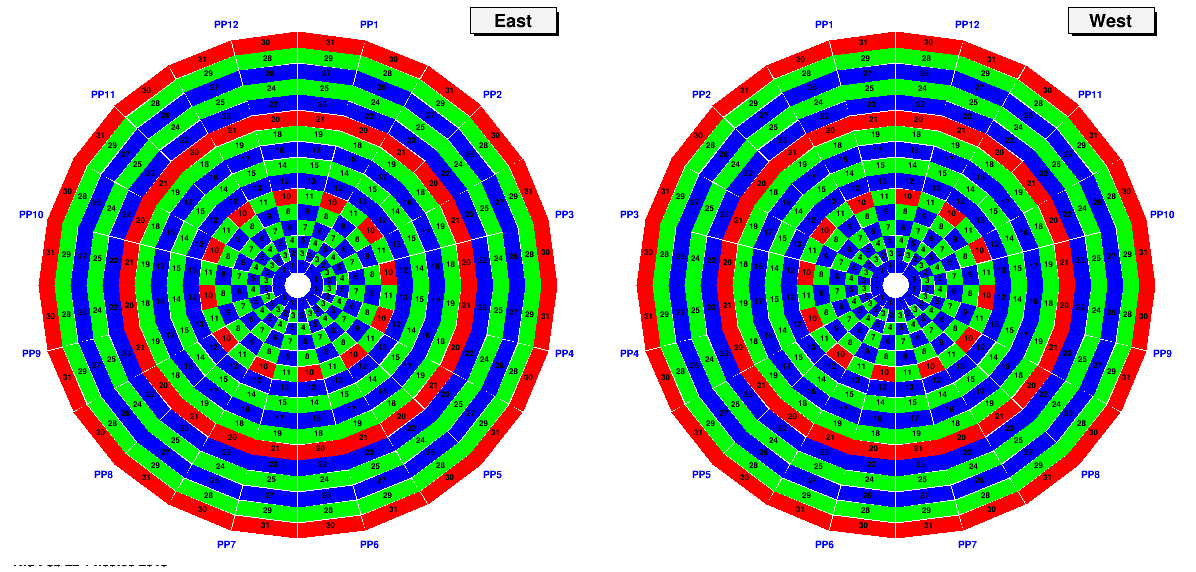
If we have passed all seven of these tests, then we can feel very safe that we are 100% correctly mapped.  Seven runs ain't bad.


Here are the run numbers (Prashanth and Joey)