Home » Blogs » skk317's blog

EPD Centrality Using UrQMD Simulation Data

Updated on Wed, 2020-03-25 09:52. Originally created by skk317 on 2020-03-25 09:52.

 Please see Mike Lisa's blog here for details on this analysis.

Ring Weights for UrQMD Au+Au 27 GeV

I used a linear fit function with mean-squared-error to find the best fit. This was done using Keras/TensorFlow in Python with a single neuron. The inputs are the 16 EPD rings, using the sum of all nMIP values in a ring per event. These are fit to the impact parameter, B, which was in the range of 3.0-10.0 fm.

The fit is of the form:

Where the wi are the weights and the ri are the ring nMIP sums. BEPD is the impact parameter found by the weighted sum. Weights are as follows:

1.767241954803466797e-01,
2.769147418439388275e-02,
1.836555637419223785e-02,
1.213719882071018219e-02,
7.054544519633054733e-03,
3.190962597727775574e-03,
-1.420150161720812321e-03,
-2.172370441257953644e-03,
-4.689844325184822083e-03,
-6.124939769506454468e-03,
-6.782258860766887665e-03,
-7.302306592464447021e-03,
-7.344271987676620483e-03,
-8.048787713050842285e-03,
-7.758192718029022217e-03,
-8.569823578000068665e-03

Here are some plots of the fits:

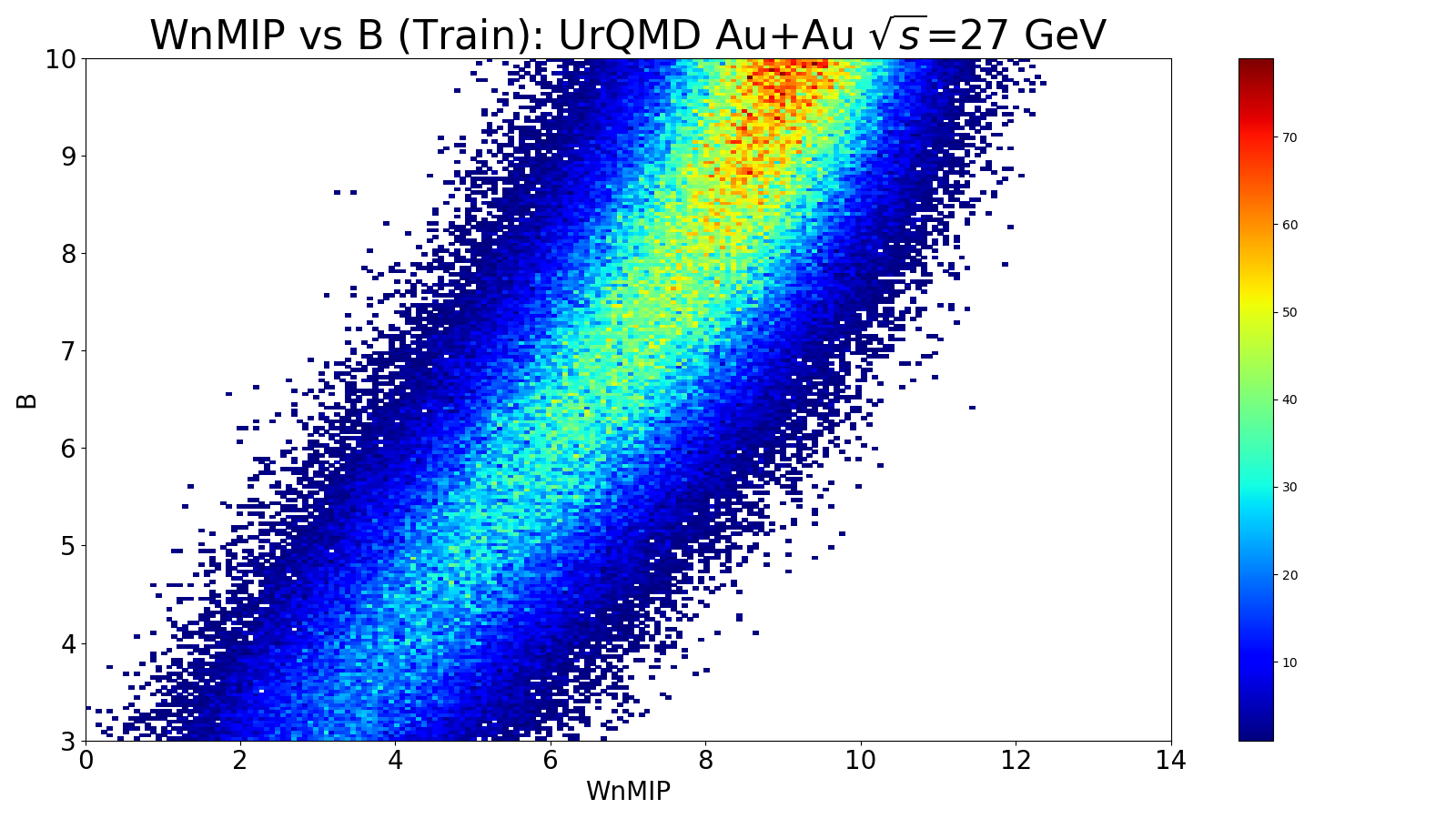
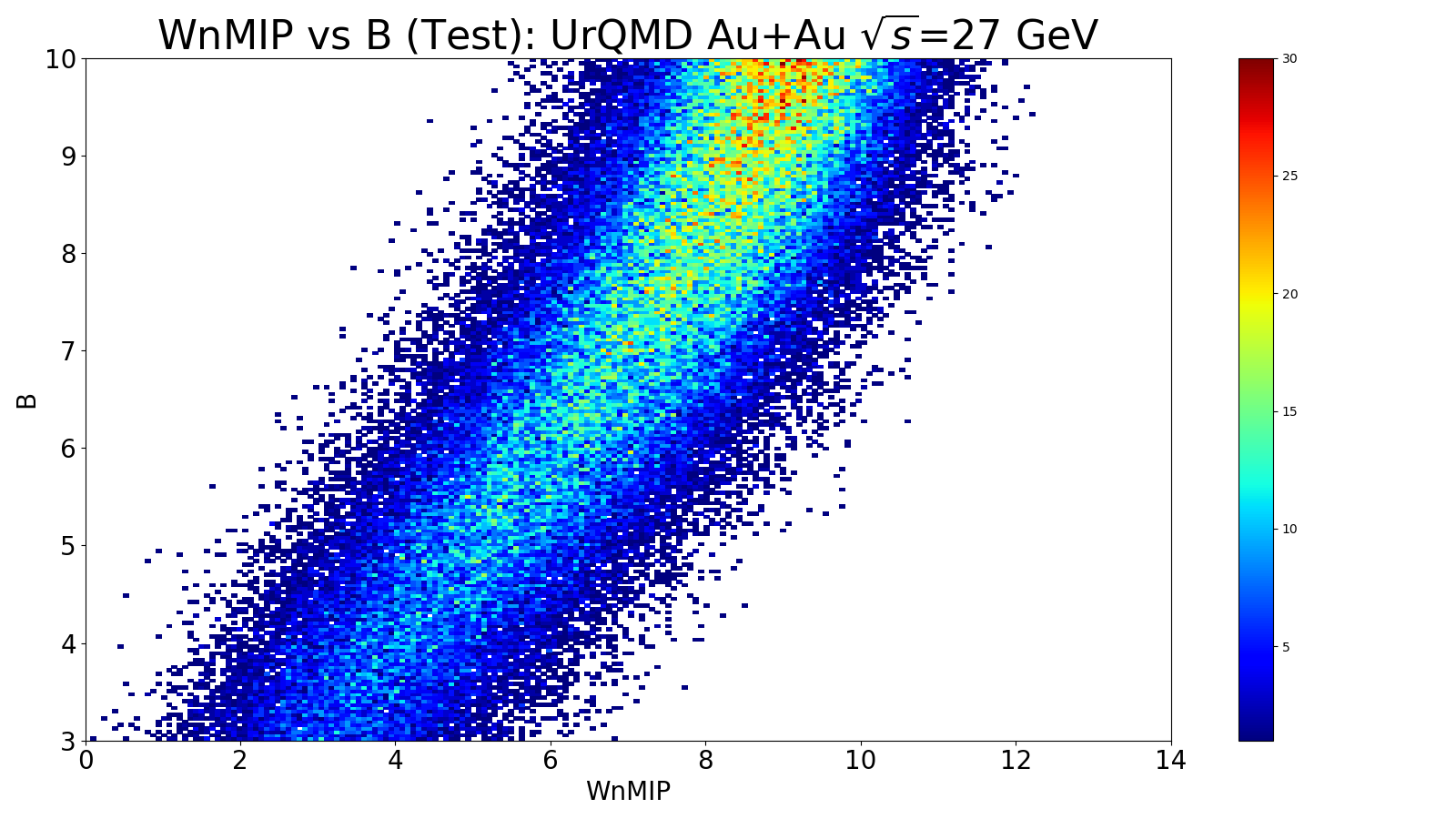
Figure 1: Data used to train the fit is on the left, and data used to test is on the right.


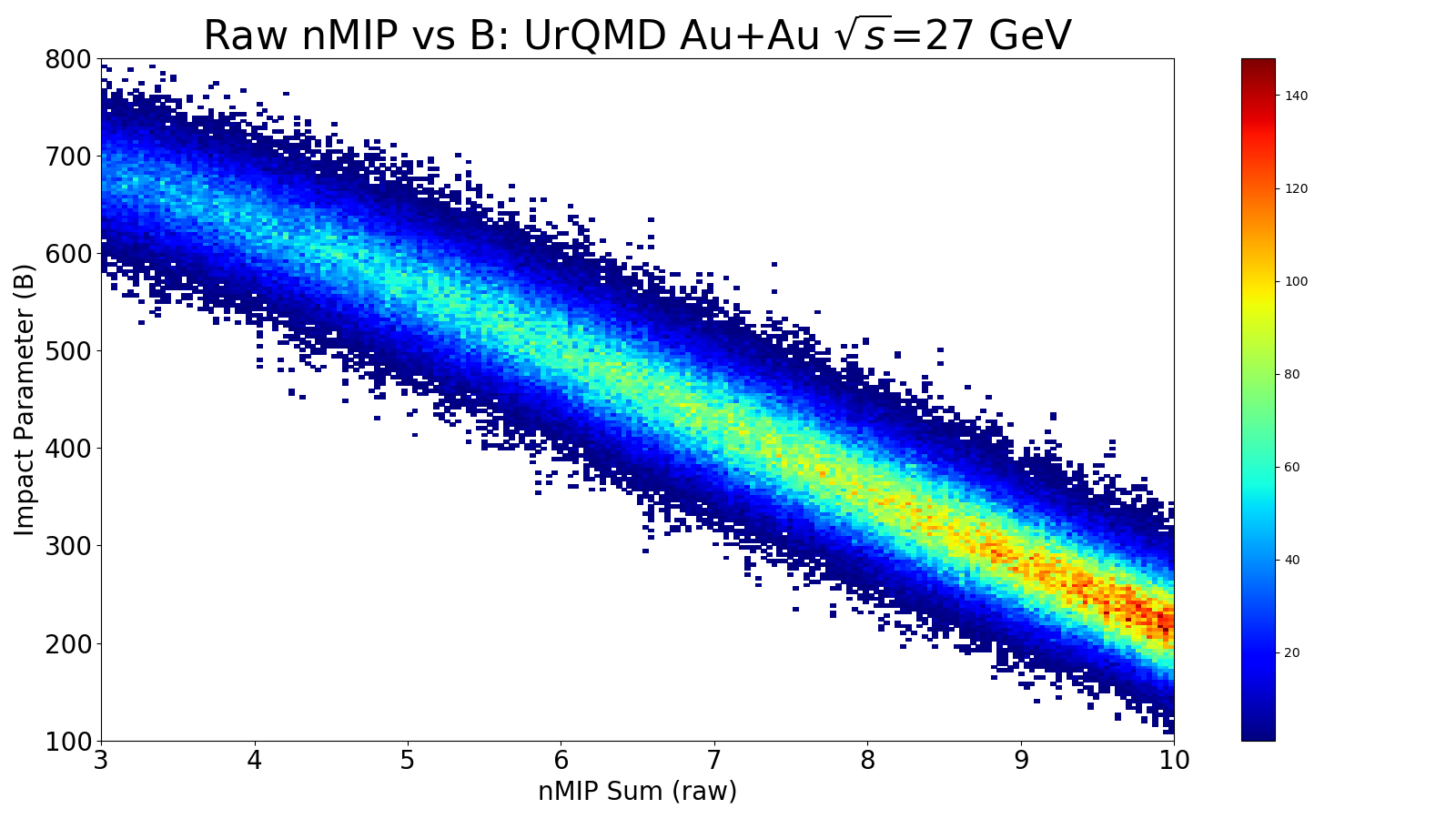
Figure 2: This is the raw nMIP sum (no weights; just summed over the entire EPD) vs impact parameter.

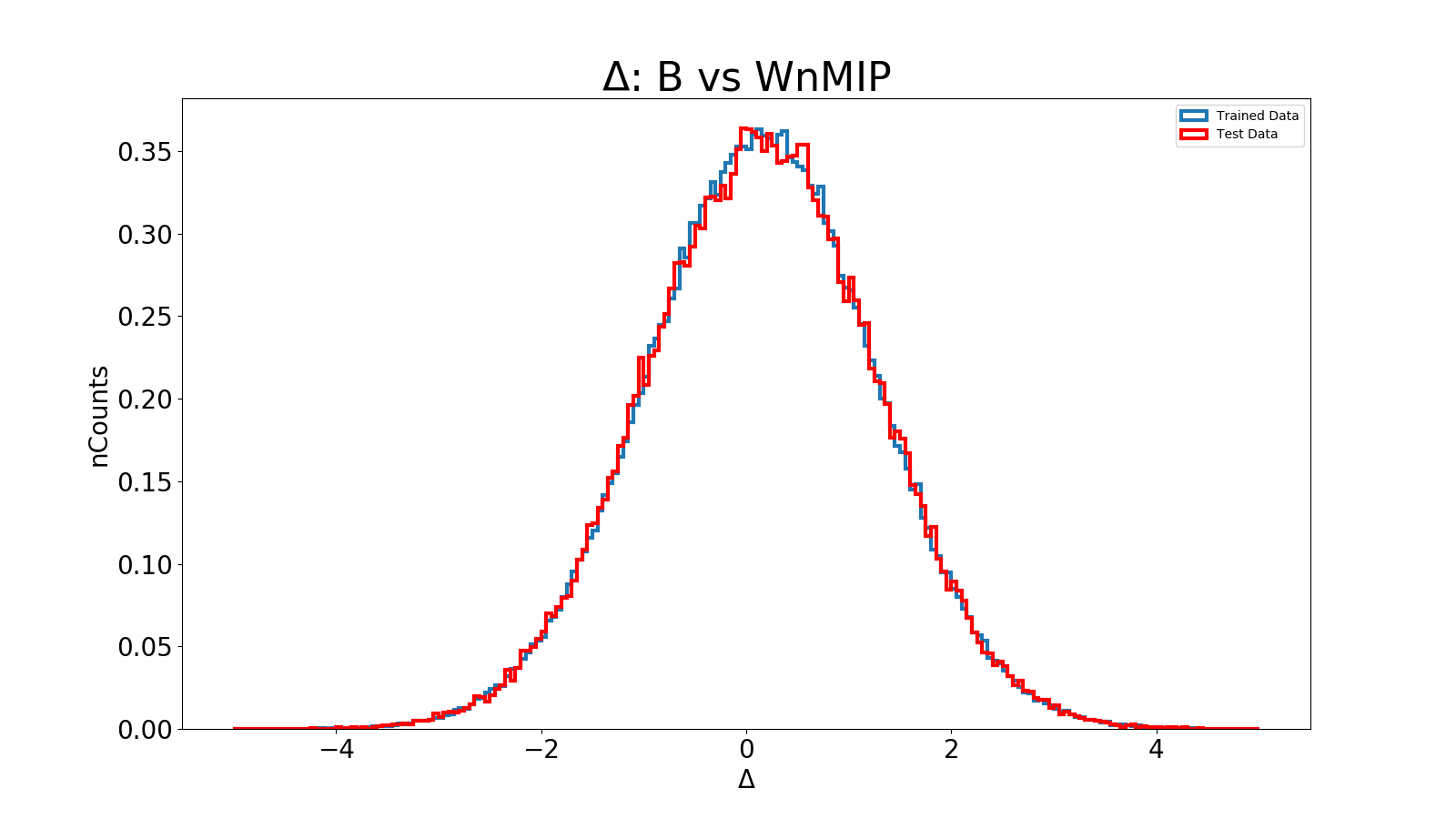
Figure 3: This is the difference between B and BEPD. The red curve is for the test data, and the blue curve for trained data.

»