I studied the rho+ reconstruction with 10M pythia+GSTAR simulation events.

    1, energy deposited efficiency

     from GSTAR simulation I get the energy deposit efficiency of pi+ and photon under the condition that I only fire the particles to the center of the south FHC.

     So, I just recorded the energy deposited in the FMS for photons and the energy deposited in the FMS+FHC for the pi+.

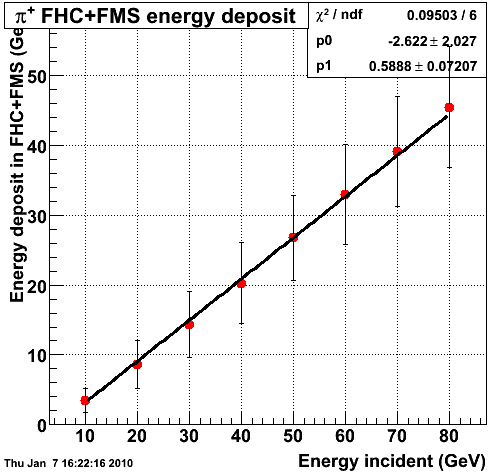
Fig1, energy (deposited in FHC+FHC) VS the incident energy of pi+

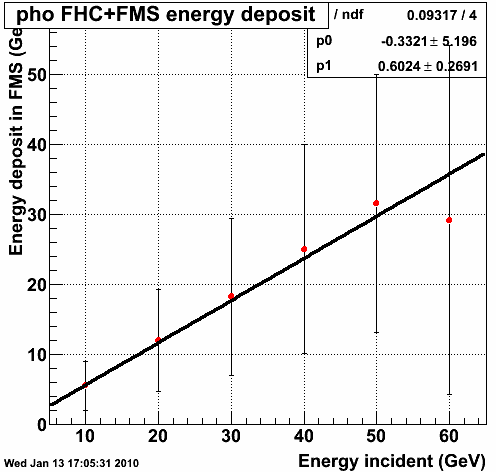
Fig2, energy (deposited in the FMS) VS the incident energy of photon

      From the above two plots, I select the following formulas to get the total energy from the deposied energy in simulation,

      For pi+,

                      E_par=(E_FMS+E_FHCN+E_FHCS+0.622)/0.65

      where E_par is the incident total energy of pi+, E_FMS is the energy deposited in the FMS of the pi+, E_FHCS(E_FHCN) is the energy deposited in the south(north) FHC of the pi+.

      For photon,

                     E_par=(E_FMS+0.3321)/0.8024

        where E_par is the incident total energy of photon, E_FMS is the energy deposited in the FMS of the photon.

      Here, I should keep in mind the energy deposited efficiency is from GSTAR simulation that the particle fired to the center of the FHC, so this is not the real energy efficiency. From the following energy comparation plots, the formulas are fine for current simulation.

    2, pythia+GSTAR simualtion data.

      (1) cuts

            * the highest tower of pi+ in the FHC position limitation ( excluding the edge cells of the FHC)

            * the photon should be in the circular which has a radius of 30cm centered in the pi+ position in the FMS (using energy weighted positions).

         * the energy weighted position in the FMS of the photon should not in the edge of the FMS.

          * the energy deposited in the FMS+FHC of pi+ is larger than 2GeV.

       (2) results

       Differences between the incident total energy and the E_par.

Fig3, the distribution of E_incident-E_par of pi+

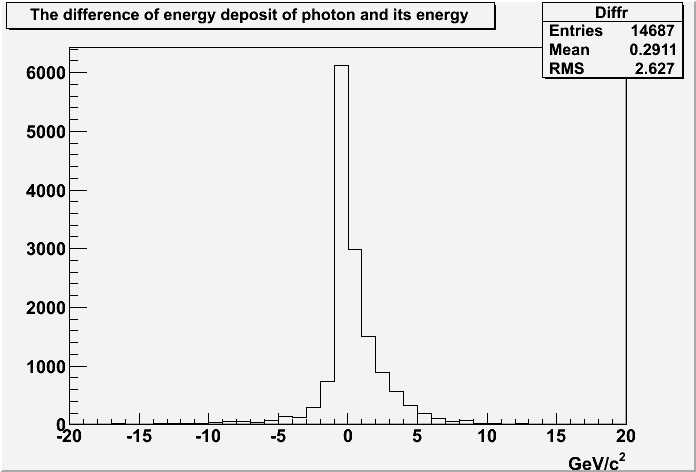
Fig4, the distribution of E_incident-E_par of photon

           The mass of the 2 photons invariant mass under a cut of |m_pair-Mpi0|<0.5.

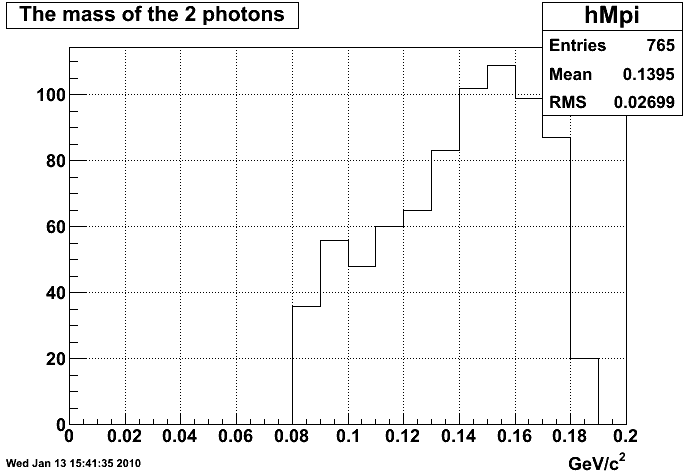
Fig5, the invariant of the photon pairs.      

          The mass of the reconstructed rho+.

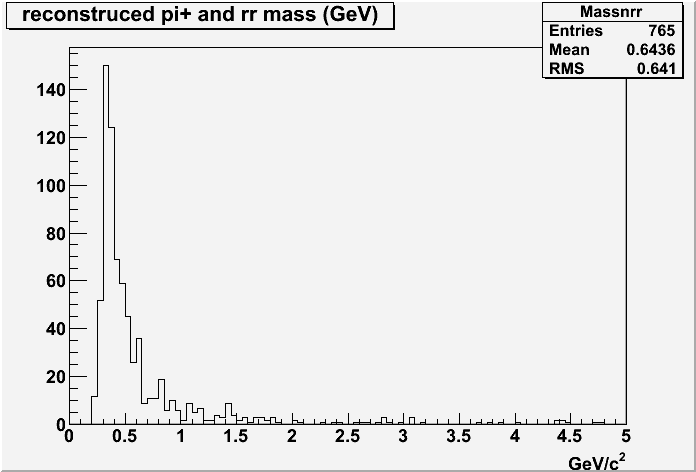
Fig6, the reconstructed mass of the rho+