- drach09's home page
- Posts
- 2022
- 2020
- June (1)
- 2019
- 2018
- 2017
- 2016
- 2015
- 2014
- December (13)
- November (2)
- October (5)
- September (2)
- August (8)
- July (9)
- June (7)
- May (5)
- April (4)
- March (4)
- February (1)
- January (2)
- 2013
- December (2)
- November (8)
- October (5)
- September (12)
- August (5)
- July (2)
- June (3)
- May (4)
- April (8)
- March (10)
- February (9)
- January (11)
- 2012
- 2011
- October (1)
- My blog
- Post new blog entry
- All blogs
Run-11 Transverse Jets: Fine Bins vs. Single Bin
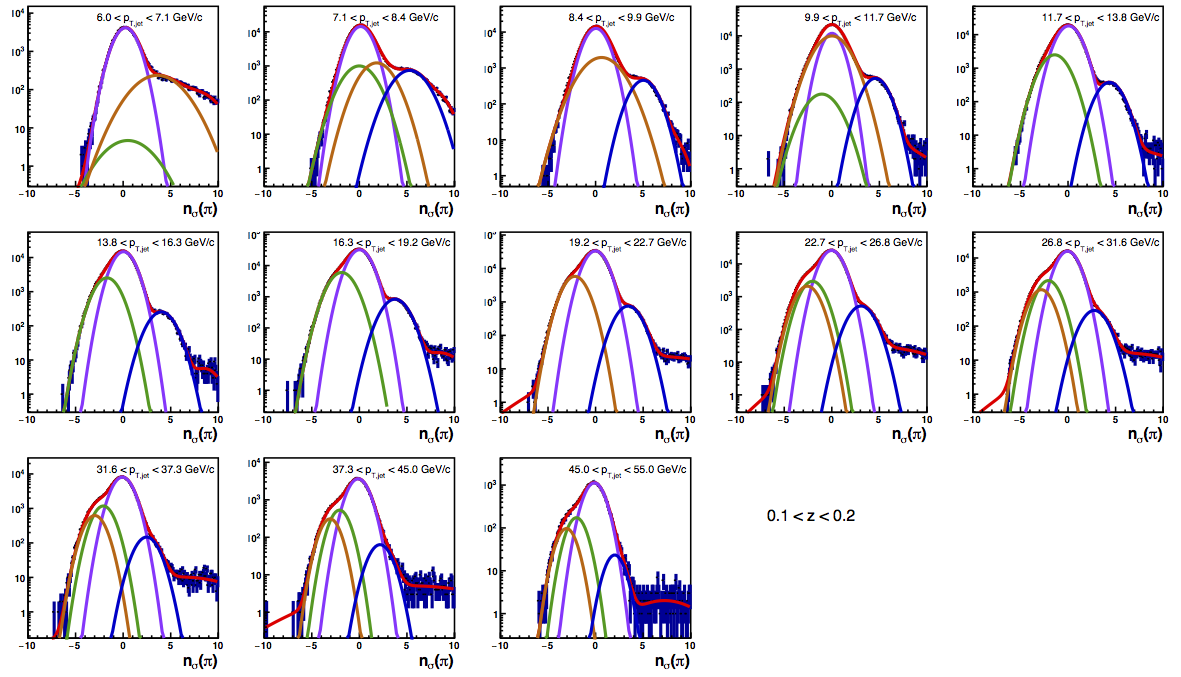
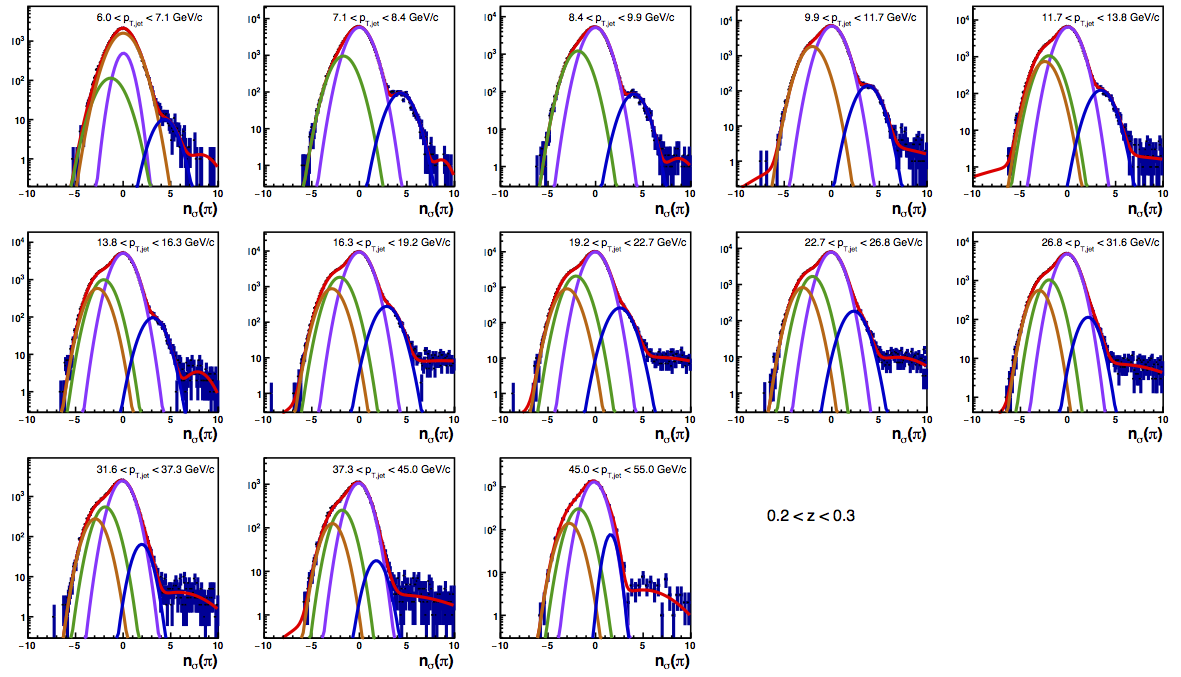
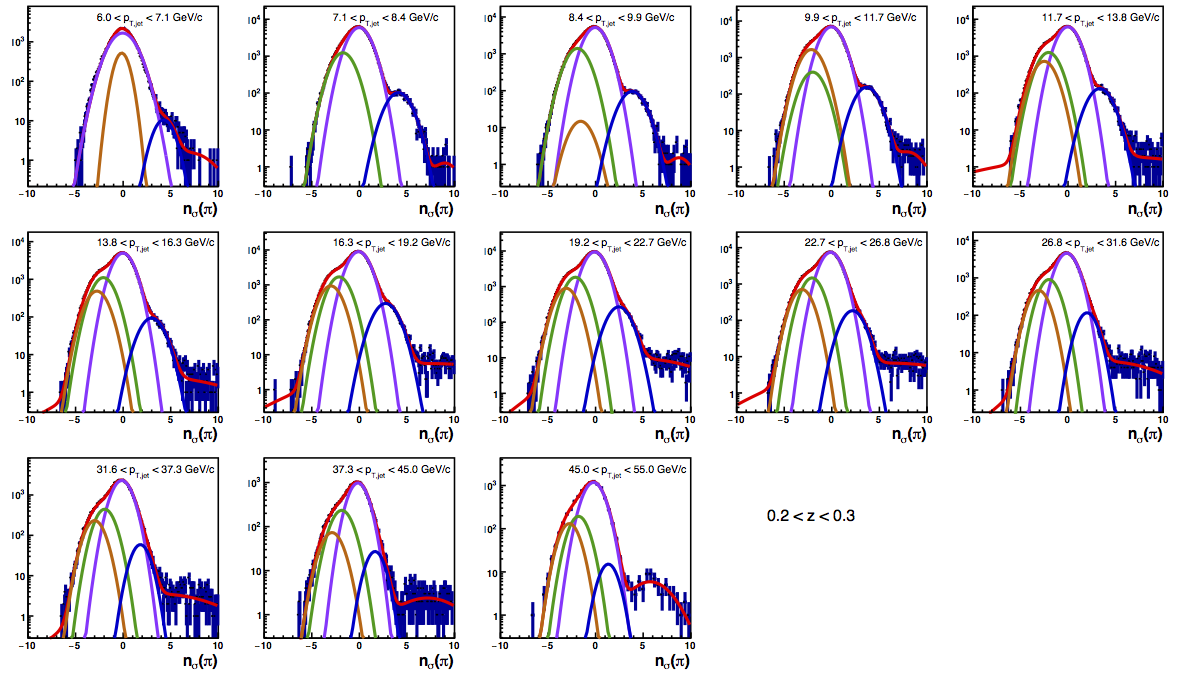
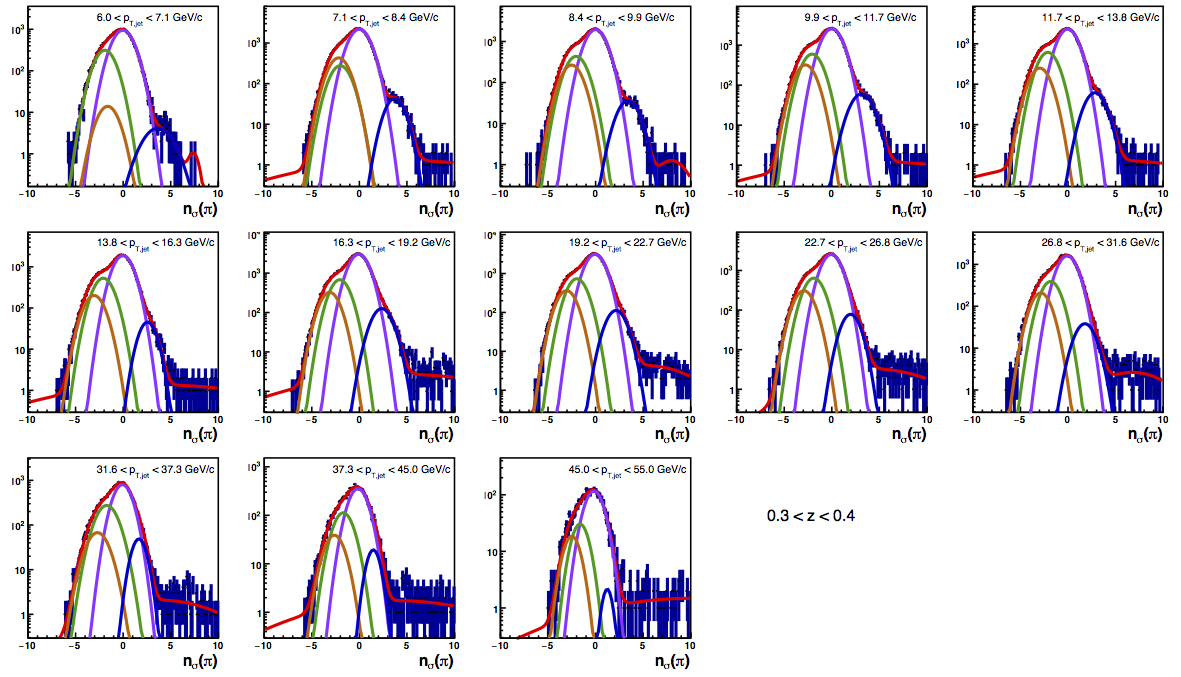
I updated the background correction for high-pT. I now use the signal fractions and covariances from the charge-separated five-Gaussian fits. To correct the background, I extract the pion, kaon, and proton asymmetries from asymmetries measured for three ranges of nσ(π). I compare the pion asymmetry results using signal fractions calculated from averaging over fine bins of jet pT to those using signal fractions from a single, course bin of jet pT. For these results, there is no systematic included for the background correction.
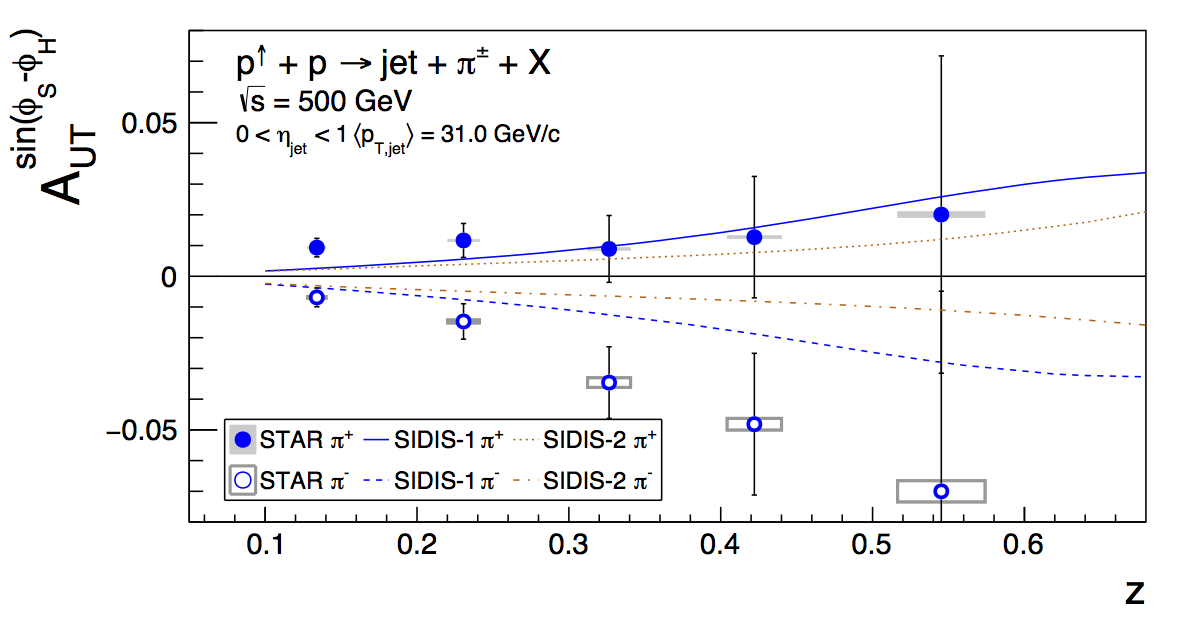
Figure 1
| Fine pT Bins | Single pT Bin |
 |
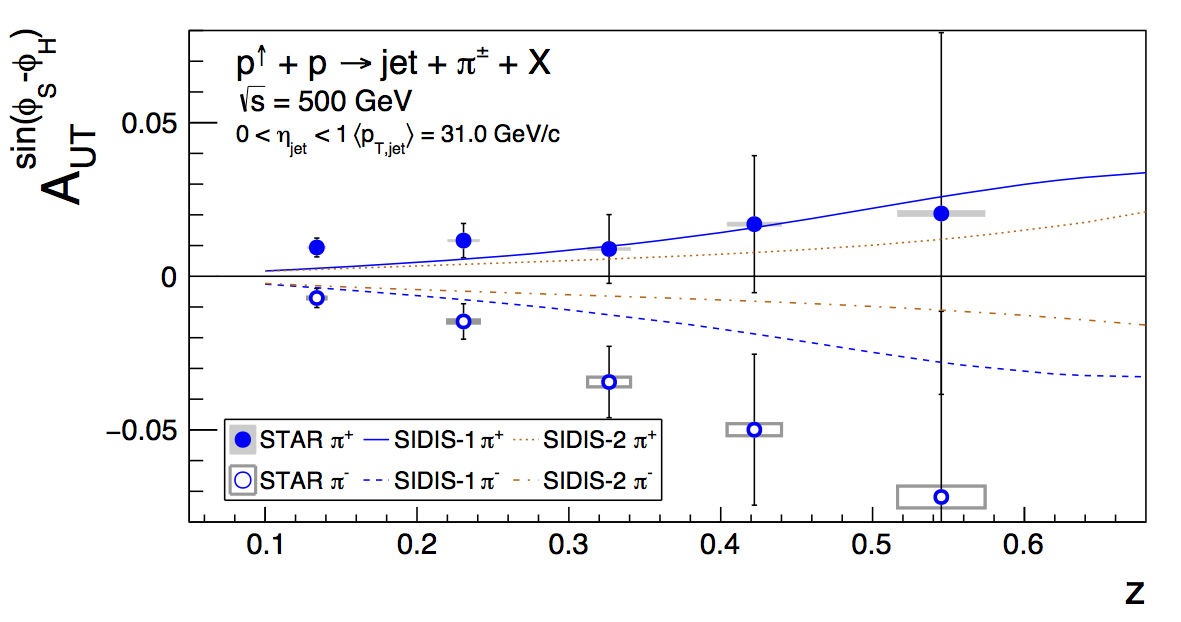 |
Qualitatively, the results are very similar. In the end, the results from the fine-pT-bin average are ever-so-slightly more precise. This is probably due to the fact that the coarse bin fractions are slightly lower, leading to a slightly larger enhancement of the statistical uncertainties. Thus, against my initial intuition, I am now inclined to go with the fine bins.
Changes from Earlier Result
There are slight changes in the results with the new background-correction procedure. A side-by-side comparison is shown in Fig. 2.
Figure 2
| New (Fine pT Bins) | Old |
 |
 |
One can see that the points have shifted slightly from earlier. This is to be expected. In addition to updated signal fractions and the three PID-range correction procedure, I also tightened up the "pion rich" PID range. This probably has the effect of reducing the precision a bit with the upside that it is a more "pure" sample. The two main things I notice are that the first z-bin of π- moves away from the horizontal a bit. This actually brings its magnitude much closer to that of π+, which seems right to me. The other thing I notice is that the shape of the z-dependence seems closer to what we expect from the model calculations. While the magnitude still does not agree terribly well in π-, the shape tracks a bit better, now.
Figure 3
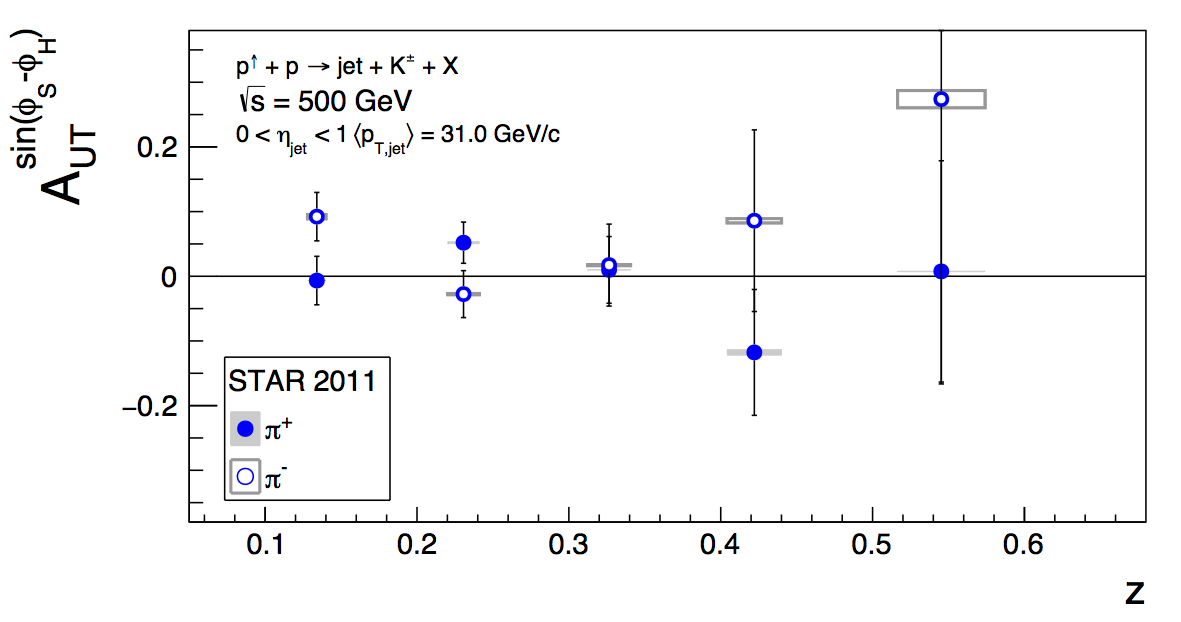
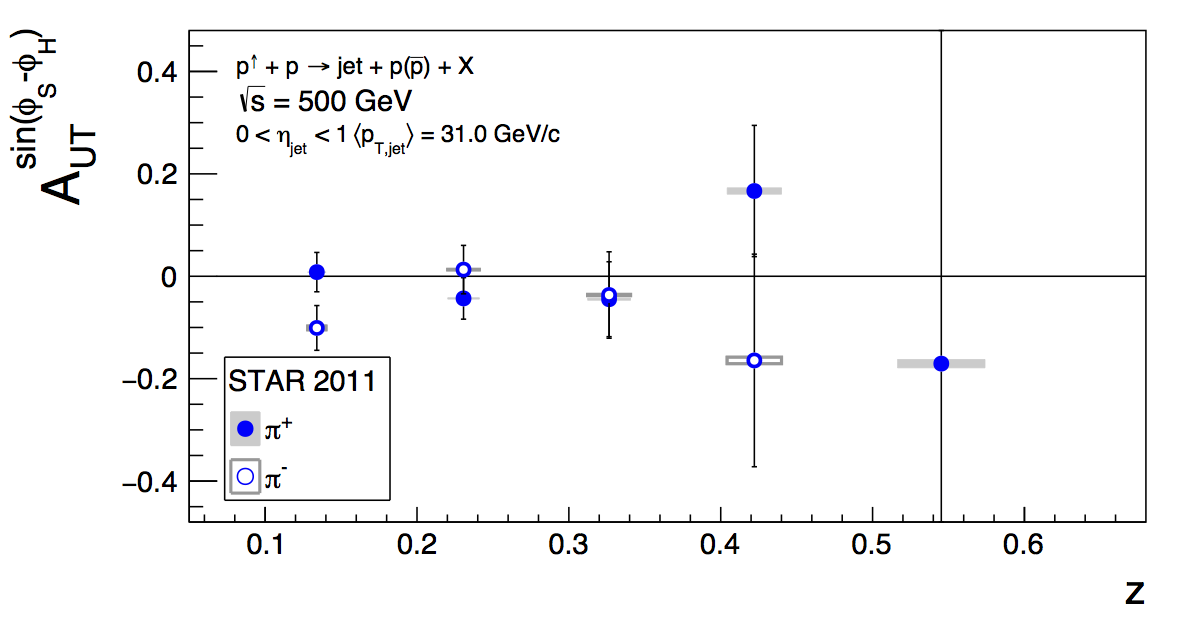
In Fig. 3, I show the nominal kaon and proton asymmetries. These essentially come for free in extracting the pion asymmetries. The statistical uncertainties are significantly larger than the pions, which clearly preclude teasing out a nonzero result.
Figure 4: PID Fits
| Positive Charge | Negative Charge |
 |
 |
 |
 |
 |
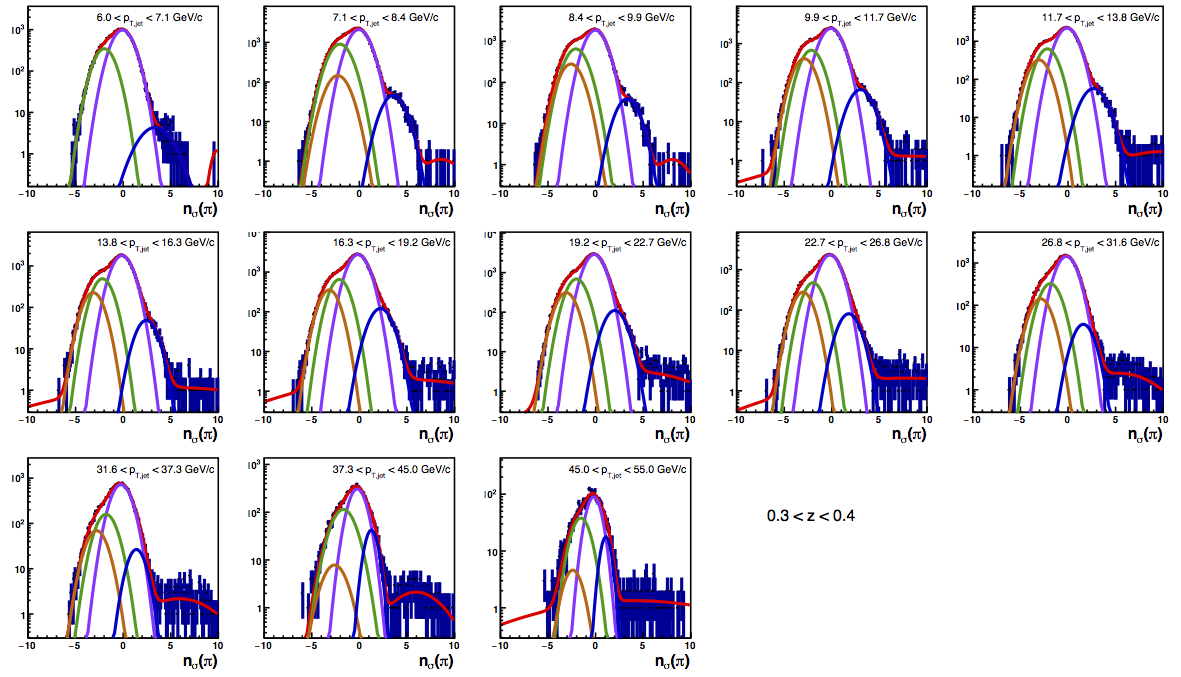 |
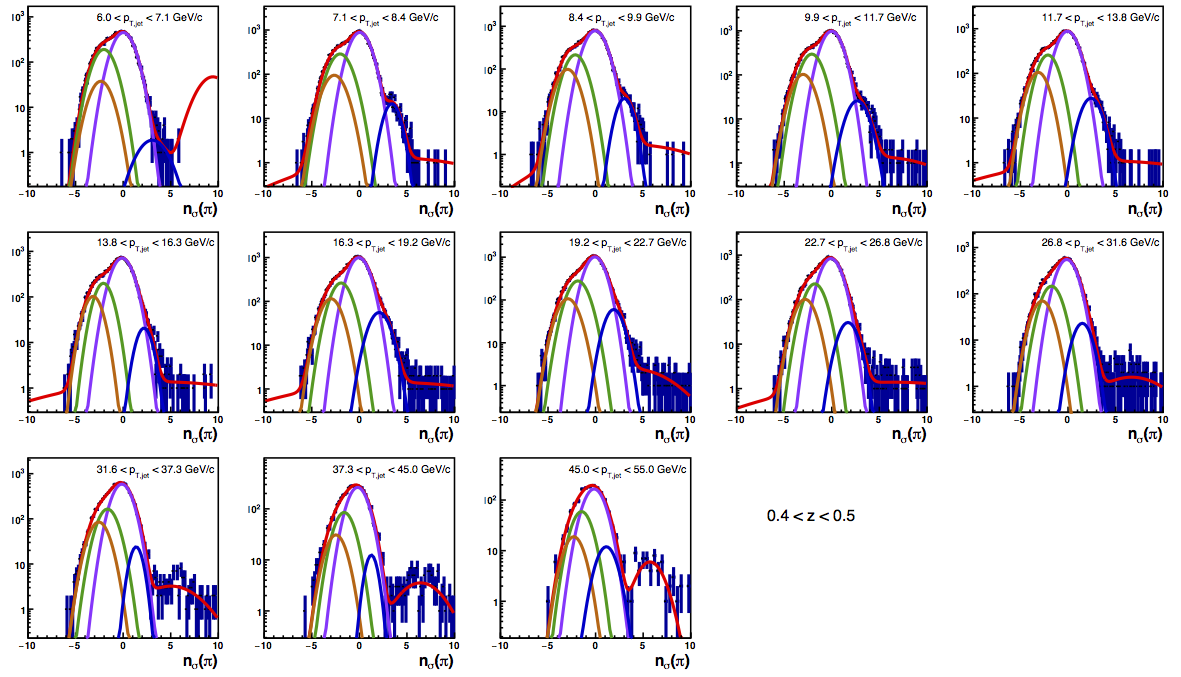 |
 |
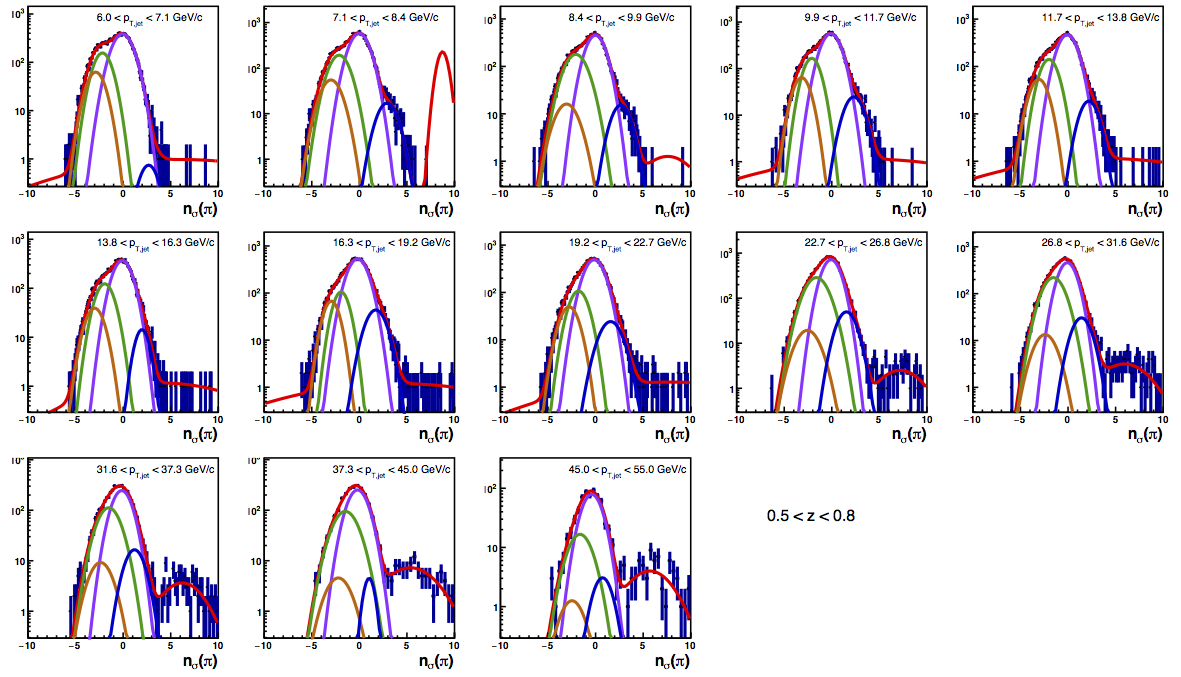 |
 |
- drach09's blog
- Login or register to post comments
