Home » Blogs » jwebb's blog

Comparison with Cross Sections

Updated on Wed, 2008-03-26 17:40. Originally created by jwebb on 2008-03-24 13:30.

Abstract:  We cross check prompt-photon yields against "known" cross sections, based on pythia expectations.  The extracted yields are found to be within a factor of two of what pythia predicts.

We cross check the results of the conversion method (both with the tight hadronic veto cuts, and the looser SMD energy ratio cuts (see section 3 in the link)) against the expected cross sections from perturbative QCD. The goal here is to determine if we are even close to being in the right ball park.

Figure 1 -- pT spectrum for photons extracted using the EEmc Gammas via conversion method.  At left we use the cuts described in the link.  At right, we remove the postshower (hadronic veto) cut and replace it with a cut on E(smd)/E(candidate).

 

 
1. Determine absolute luminosities for the runs used to calculate gamma yields
     a. Run list used in the analysis
     b. Jamie's bytrig.pl perl script used to sum up luminosities for each trigger, by each day, etc...
     $ bytrig.pl -s -f -r runlist.txt

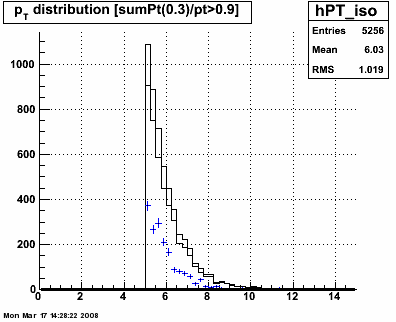
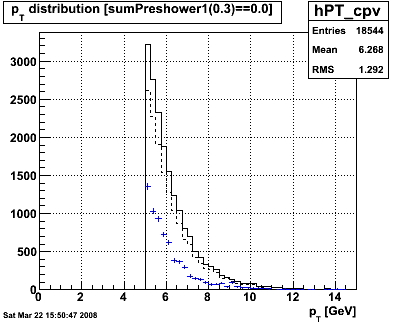
 Result: trigger ID 137641 / aka EEMC L2gamma accumulated 4.3 pb-1.  FOM is 0.27 pb-1 based on online polarizations.

 
2.  For a luminosity of 4.3 pb-1, how many events do we expect vs. pT?  First try a quick pythia simulation.
     a. Use pythia 8.1000
     b. Set min partonic pT = 4 GeV (to speed calculation)
     c. Select only direct gamma processes
     d. Count event if pT > 5 GeV and 1.05 < eta < 2.0
     e. Accumulate a sample of 6800 events

Result:  6800 events in EEmc above pT = 5 GeV for Ntried = 232468 σ = 1.557 times 105 mb. Luminosity = 1.49 pb-1.

Expect 19,624 gammas in EEmc acceptance with pT > 5 GeV for 4.3 pb-1.
Expect 10,090 gammas in EEmc acceptance with pT > 6 GeV for 4.3 pb-1.

Figure 2 -- pT spectrum for 4.3pb-1 of data, pythia 8.100.

3. Correct measured pT spectra for detector efficiencies.
    a. Generate ~20k single gammas using Y2006 geometry
    b. Throw flat in eta and slightly wider than the EEMC acceptance, 30cm width in Z vertex (yes, it's too narrow).
    c.  Throw with a "not unreasonable" pT distribution

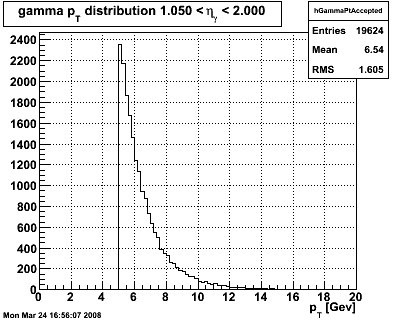
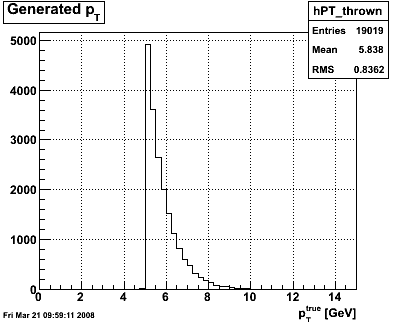
Figure 3 -- Generated pT distribution (left), acceptance, i.e. fraction of photons which hit the endcap (right).

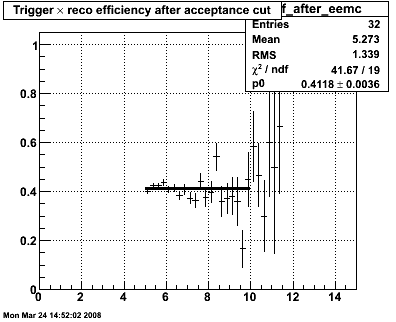
      d. Run the gamma extraction code using both sets of cuts:

Set I: Tight Cuts with Hadronic Veto

1. Require candidate w/in EEMC with pT > 5 GeV
2. Isolation Cut: Gamma candidate carries at least 90% of the E_T summed over R < 0.3
3. Hadronic Veto: Sum of postshower tiles w/in R < 0.3 is less than 0.2 MeV
4. Charged Particle Veto (CPV) Cut: Sum of preshower-1 tiles w/in R < 0.3 is equal to zero
5. Analyzing Cut: Sum of preshower-2 tiles w/in R < 0.3 is greater than zero

Set II: Loose cuts with SMD ratio cut

1. Require candidate w/in EEMC with pT > 5 GeV
2. Isolation Cut: Gamma candidate carries at least 90% of the E_T summed over R < 0.3
3. SMD Energy Ratio Cut: Eu / Ecandidate > 0.0025 and Ev / Ecandidate > 0.0025
4. Charged Particle Veto (CPV) Cut: Sum of preshower-1 tiles w/in R < 0.3 is equal to zero
5. Analyzing Cut: Sum of preshower-2 tiles w/in R < 0.3 is greater than zero

 

Figure 4 -- Ratio of number of gammas passing the CPV cut to the total number generated.  Note-- to get the efficiency, we should divide by the acceptance function from figure 1.  Set I (left), set II (right).

 

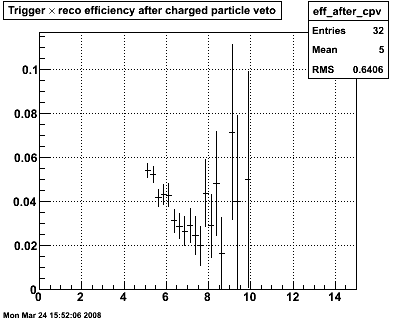
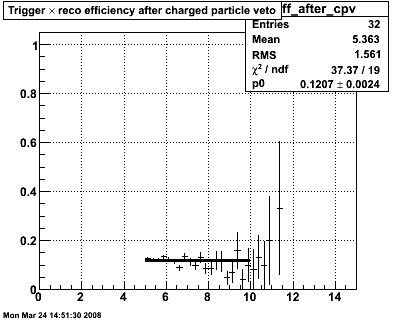
Figure 5 -- Single-gamma pT spectra for set I cuts (left) and set II cuts (right), corrected for inefficiencies.  Error bars should not be taken overly seriously at this point.  Still, set I integrates to 17.7k events.  Set II integrates to 23.6k events.

4.  Yield corrections
      a. Detector livetime.  Assume we ran at 35 Hz for the run.  35% deadtime.
      b. Geometric acceptance, specifically what fraction of the detector is essentially "dead" because of dead HW channels or too much material in frontof it?
          i. There are the "usual suspects".  Two dead towers.  2/720 dead.
          ii. There is a significant (>1 radiation length) block of aluminium in front of xxTC07, where xx=1..12.  Another 12/720 dead.
          iii. There are the spokes in the TPC, aligned w/ each EEMC sector.  Assume 1/4 of a tower-width is shadowed, thats another 36 dead.
          total acceptance correction: (40/720) =~ 5.56%.

 

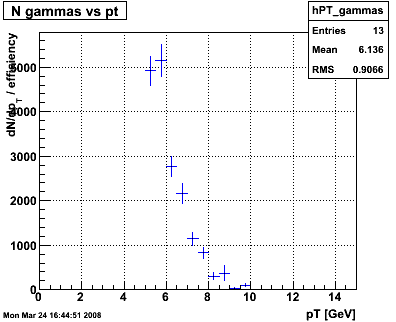
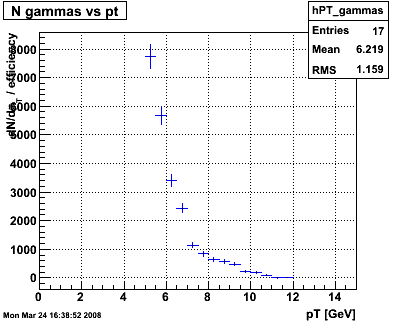
6. Tabulate yields, corrected for efficiencies, livetime, dead detectors

SET raw eff. corrected live time corrected [see note]
I 1780 17.7k 28.7k
II 6800 23.6k 38.2k
pythia -- 19.6k 19.6k

 

Conclusions:

The gamma yields extracted using the conversion method are within a factor of 2 of expectations based on pythia.

Email from Carl--
The standard luminosity estimate already includes the effects of
finite live time (assuming you used the appropriate number for slow
detector events).  Therefore, the 1/0.65 factor that you included
represents double counting.  However, correcting that won't change
your conclusion that you are at least in the right ballpark.

Carl

I assume  that Jamie's perl script already takes this into account... if so, then the comparison is with the efficiency corrected column, and the conclusion is that we are within 10-20% of the yields expected from pythia. 

»