Ilya Selyuzhenkov February 27, 2008

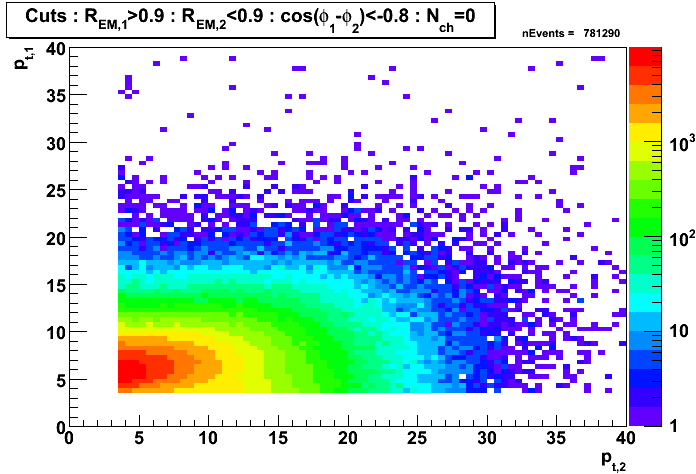
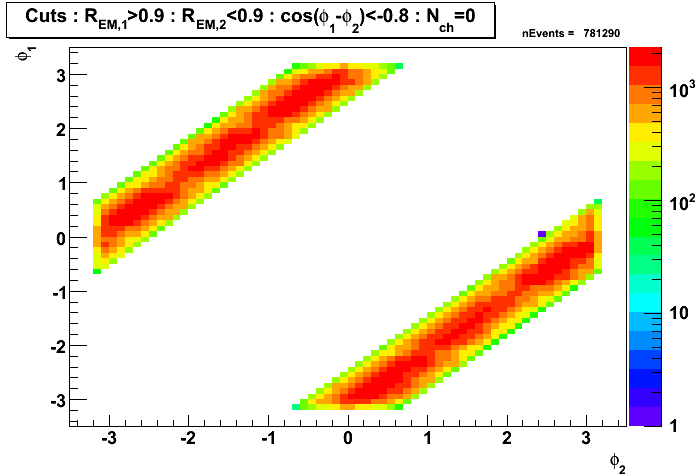
Gamma-jet candidates before applying clustering algorithm

Gamma-jet isolation cuts:

1. selecting di-jet events with the first jet dominated by EM energy,
   and the second one with a large fraction of hadronic energy:

   R_EM1 >0.9 and R_EM2 < 0.9

2. selecting di-jet events with jets pointing opposite in azimuth:

   cos(phi1 - phi2) < -0.8

3. requiring no charge tracks associated with a first jet (jet with a maximum EM fraction):

   nCharge1 = 0

Figure 1: Transverse momentum

Figure 2: Pseudorapidity

Figure 3: Azimuthal angle

Tower based clustering algorithm

• for each gamma-jet candidate finding a tower with a maximum energy
  associated with a jet1 (jet with a maximum EM fraction).

• Calculating energy of the cluster by finding all adjacent towers and adding their energy together.

• Implementing a cut based on cluster energy fraction, R_cluster, where

  R_cluster is defined as a ratio of the cluster energy
  to the total energy in the calorimeter associated with a jet1.
  Note, that with a cut Ncharge1 =0, energy in the calorimeter is equal to the jet energy.

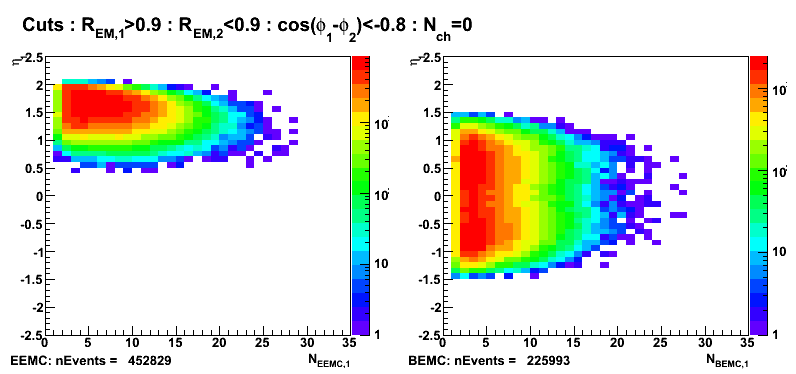
Distribution of cluster energy vs number of towers fired in EEMC/BEMC

Figure 4: R_cluster vs number of towers fired in EEMC (left) and BEMC (right). No pt cuts.

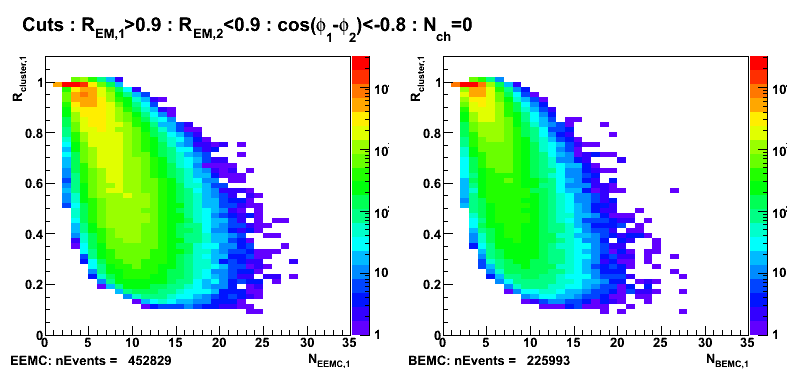
Figure 5: R_cluster vs number of towers fired in EEMC (left) and BEMC (right). Additional cut: pt1>7GeV

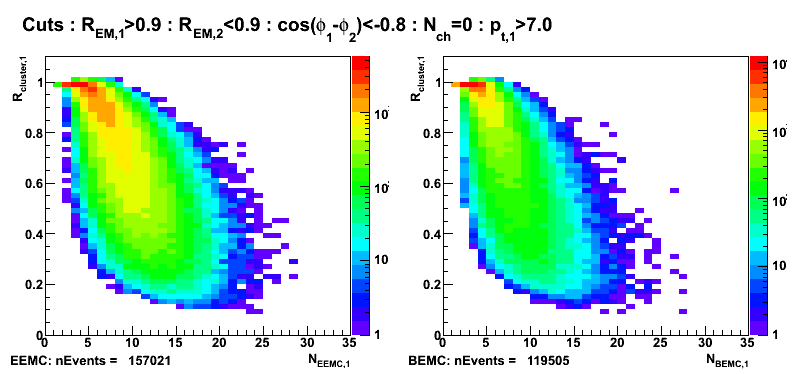
Figure 6: jet1 pseudorapidity vs number of towers fired in EEMC (left) and BEMC (right).

R_cluster>0.9 cut: EEMC vs BEMC gamma-jet candidates

EEMC candidates: nTowerFiredBEMC=0
BEMC candidates: nTowerFiredEEMC=0

Figure 7: Pseudorapidity (left EEMC, right BEMC candidates)

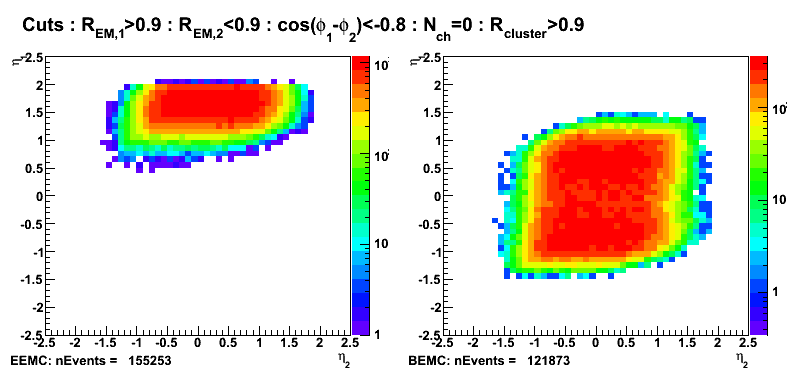
Figure 8: Azimuthal angle (left EEMC, right BEMC candidates)

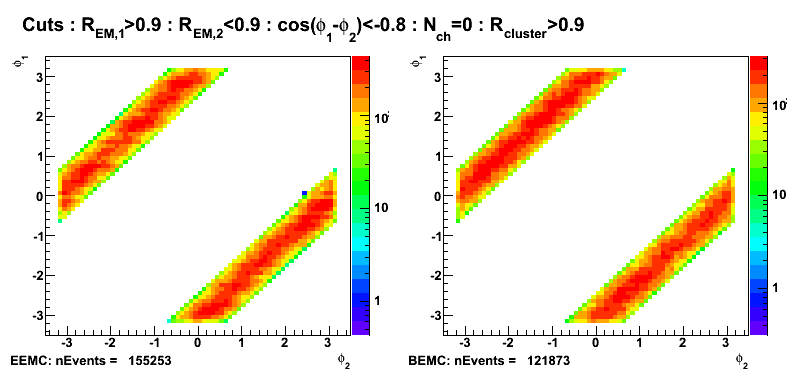
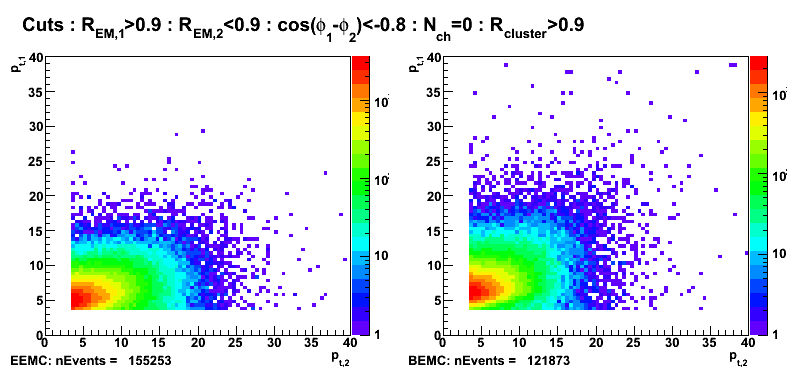
Figure 9: Transverse momentum (left EEMC, right BEMC candidates)

Number of gamma-jet candidates with an addition pt cuts

Figure 10: Transverse momentum (left EEMC, right BEMC candidates): pt1>7GeV

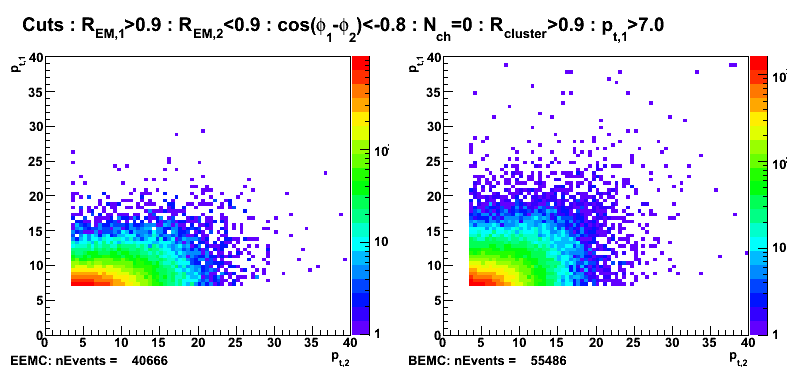
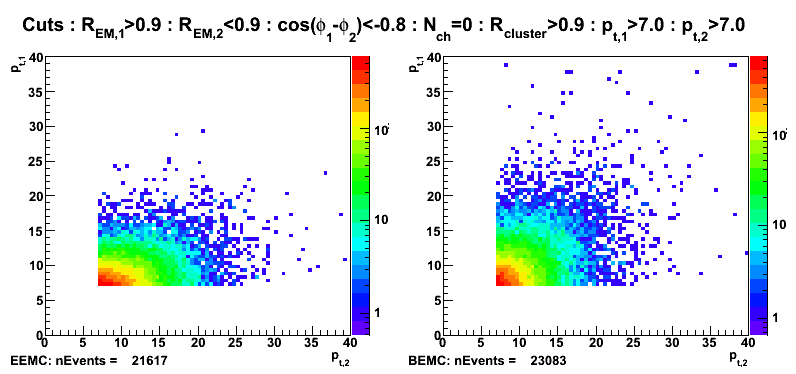
Figure 11: Transverse momentum (left EEMC, right BEMC candidates): pt1>7 and pt2>7