2008.02.27 Tower based clustering algorithm, and EEMC/BEMC candidates
Ilya Selyuzhenkov February 27, 2008
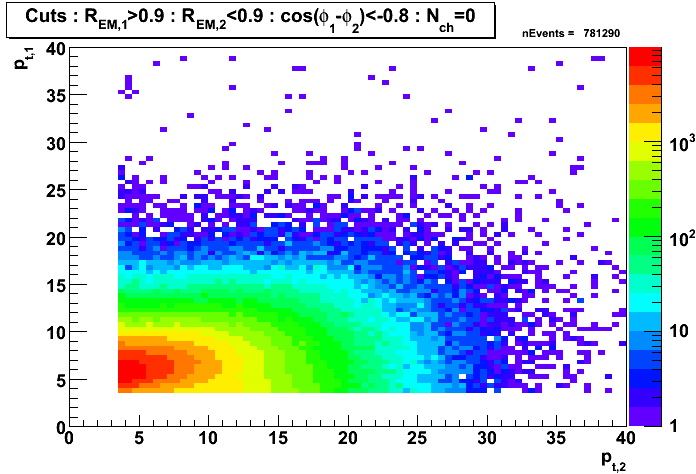
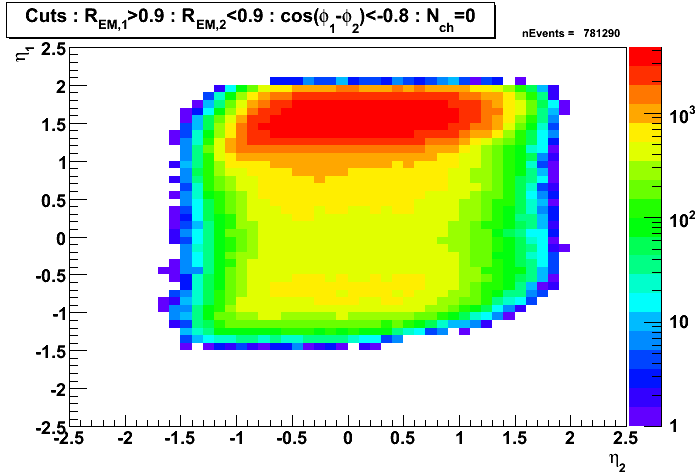
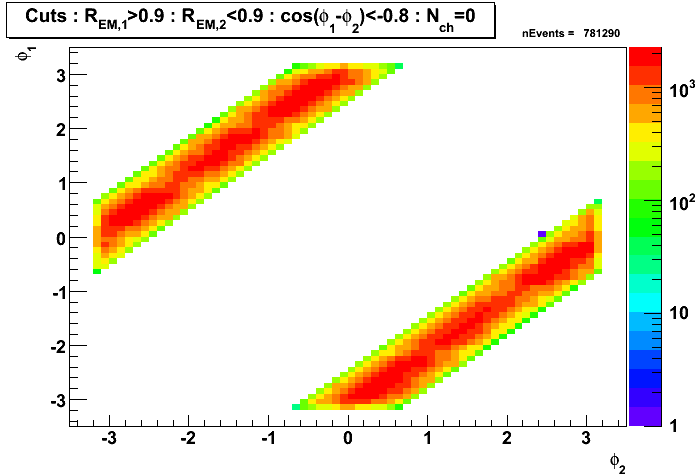
Gamma-jet candidates before applying clustering algorithm
Gamma-jet isolation cuts:
- selecting di-jet events with the first jet dominated by EM energy,
and the second one with a large fraction of hadronic energy:R_EM1 >0.9 and R_EM2 < 0.9
- selecting di-jet events with jets pointing opposite in azimuth:
cos(phi1 - phi2) < -0.8
- requiring no charge tracks associated with a first jet (jet with a maximum EM fraction):
nCharge1 = 0
Tower based clustering algorithm
-
for each gamma-jet candidate finding a tower with a maximum energy
associated with a jet1 (jet with a maximum EM fraction). -
Calculating energy of the cluster by finding all adjacent towers and adding their energy together.
- Implementing a cut based on cluster energy fraction, R_cluster, where
R_cluster is defined as a ratio of the cluster energy
to the total energy in the calorimeter associated with a jet1.
Note, that with a cut Ncharge1 =0, energy in the calorimeter is equal to the jet energy.
Distribution of cluster energy vs number of towers fired in EEMC/BEMC
Figure 4: R_cluster vs number of towers fired in EEMC (left) and BEMC (right). No pt cuts.
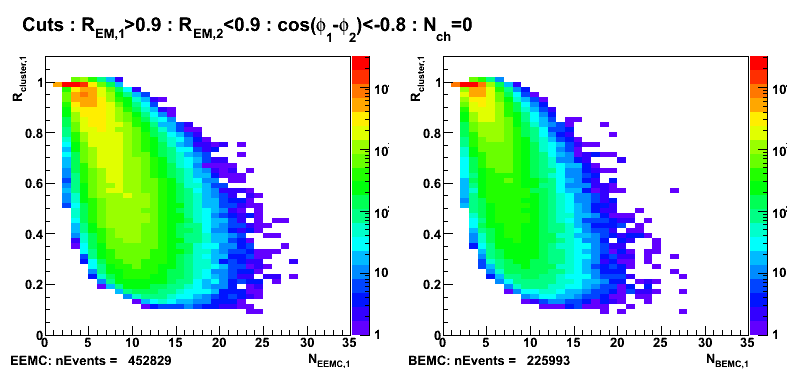
Figure 5: R_cluster vs number of towers fired in EEMC (left) and BEMC (right). Additional cut: pt1>7GeV
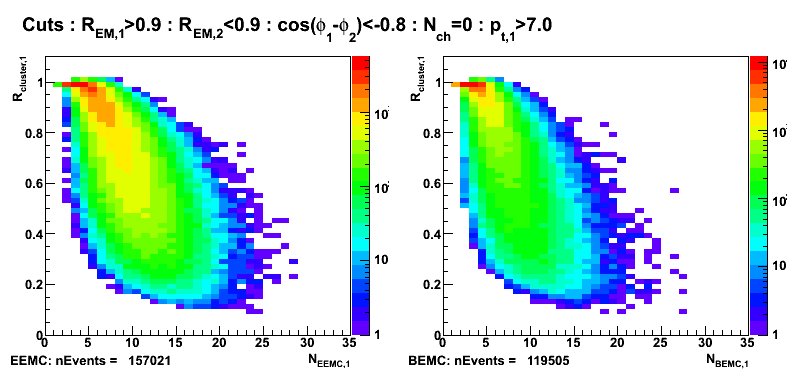
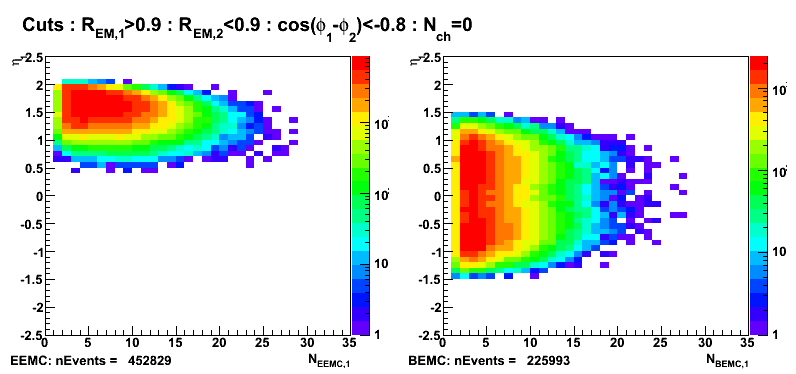
Figure 6: jet1 pseudorapidity vs number of towers fired in EEMC (left) and BEMC (right).
R_cluster>0.9 cut: EEMC vs BEMC gamma-jet candidates
EEMC candidates: nTowerFiredBEMC=0
BEMC candidates: nTowerFiredEEMC=0
Figure 7: Pseudorapidity (left EEMC, right BEMC candidates)
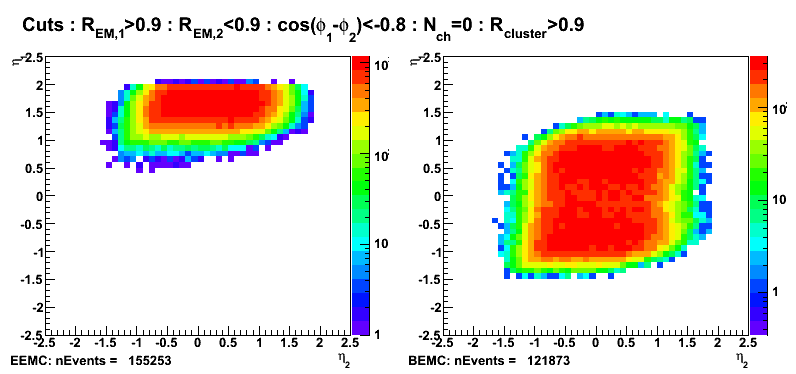
Figure 8: Azimuthal angle (left EEMC, right BEMC candidates)
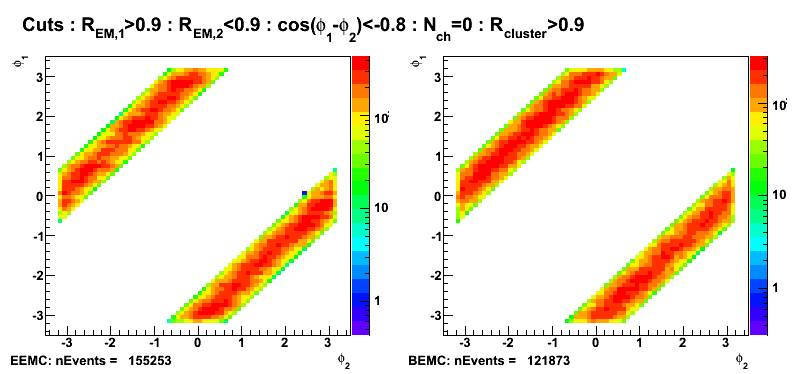
Figure 9: Transverse momentum (left EEMC, right BEMC candidates)
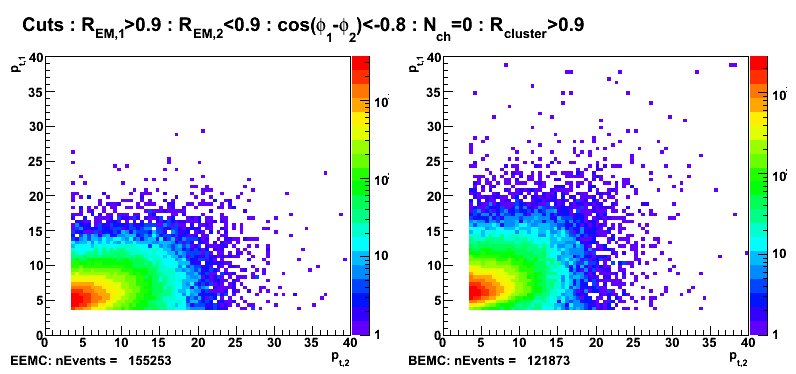
Number of gamma-jet candidates with an addition pt cuts
Figure 10: Transverse momentum (left EEMC, right BEMC candidates): pt1>7GeV
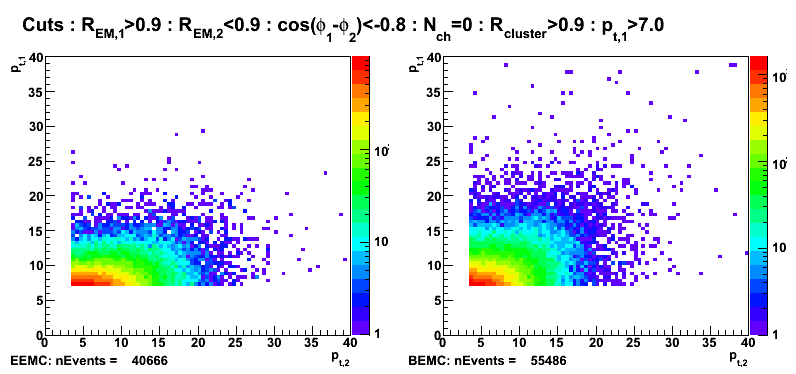
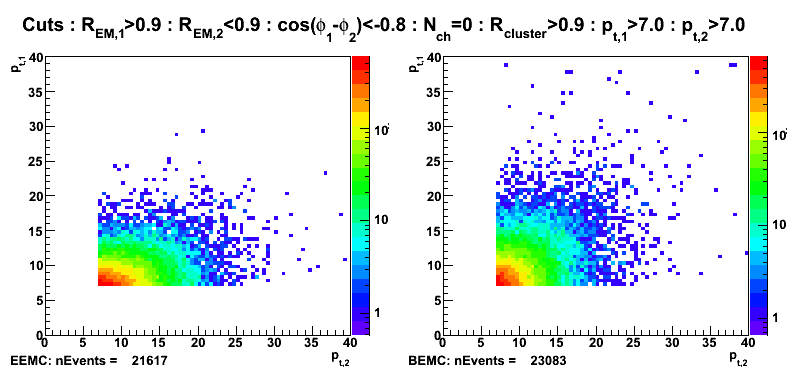
Figure 11: Transverse momentum (left EEMC, right BEMC candidates): pt1>7 and pt2>7
- Printer-friendly version
- Login or register to post comments