- Bulk correlations
- Common
- GPC Paper Review: ANN-ASS pp Elastic Scattering at 200 GeV
- Hard Probes
- Heavy Flavor
- Jet-like correlations
- LFS-UPC
- Measurement of Single Transverse Spin Asymmetry, A_N in Proton–Proton Elastic Scattering at √s = 510 GeV
- Other Groups
- Peripheral Collisions
- Spin
- Spin PWG
- Results and data
- Spin/Cold-QCD Older Physics Analysis
- 2006 EEMC Neutral Pion Cross Section and A_LL
- 2006 Gamma + Jet
- 2009 Lambda D_LL @ 200 GeV
- 2009 dijet x-sect/A_LL @ 200 GeV
- 2011 FMS Jet-like correlations @ 500 GeV
- 2011 FMS inclusive pions @ 500 GeV
- 2011 IFF @ 500 GeV
- 2011 Pions in Jets A_UT @ 500 GeV
- 2012 EEMC Neutral Pion A_LL
- 2012 IFF @ 200 GeV
- 2012 Jet A_LL @ 500 GeV
- 2012 Lambda D_TT @200GeV
- 2012 Pi0 - Jet A_LL @ 500
- 2012 Pions in Jets A_UT @ 200 GeV
- 2012 dijet A_LL @ 500
- 2012/13 FMS A_LL @ 500 GeV
- 2013 Di-jet A_LL @ 500 GeV
- A New Users Guide to PDSF Success
- Analyses from the early years
- (A) List of Physics Analysis Projects (obsolete)
- Common Analysis Trees
- EEMC Direct Photon Studies (Pibero Djawotho, 2006-2008)
- 2006.07.31 First Look at SMD gamma/pi0 Discrimination
- 2006.08.04 Second Look at SMD gamma/pi0 Discrimination
- 2006.08.06 Comparison between EEMC fast and slow simulator
- 2006.09.15 Fit Parameters
- 2007.02.05 Reconstructed/Monte Carlo Photon Energy
- 2007.02.08 E_reco / E_mc vs. eta
- 2007.02.11 Reconstructed/Monte Carlo Muon Energy
- 2007.02.15 160 GeV photons
- 2007.02.15 20 GeV photons
- 2007.02.15 80 GeV photons
- 2007.02.15 Reconstructed/Monte Carlo Electron Energy
- 2007.02.19 10 GeV photons
- 2007.02.19 40 GeV photons
- 2007.02.19 5 GeV photons
- 2007.02.19 Summary of Reconstructed/Monte Carlo Photon Energy
- 2007.05.24 gamma/pi0 separation in EEMC using linear cut
- 2007.05.24 gamma/pi0 separation in EEMC using quadratic cut
- 2007.05.24 gamma/pi0 separation in EEMC using quadratic cut
- 2007.05.30 Efficiency of reconstructing photons in EEMC
- 2007.06.12 gamma/pi0 separation in EEMC at pT 5-10 GeV
- 2007.06.28 Photons in Pythia
- 2007.07.09 How to run the gamma fitter
- 2007.07.25 Revised gamma/pi0 algorithm in 2006 p+p collisions at sqrt(s)=200 GeV
- 2007.09.12 Endcap Electrons
- 2008.01.23 Endcap etas
- 2008.02.27 ESMD shape library
- 2008.02.28 ESMD QA for run 7136033
- 2008.03.04 A second look at eta mesons in the STAR Endcap Calorimeter
- 2008.03.08 Adding the SMD energy to E_reco/E_MC for Photons
- 2008.03.21 Chi square method
- 2008.04.08 Data-Driven Shower Shapes
- 2008.04.12 Data-Driven Residuals
- 2008.04.12 Pythia Gamma-Jets
- 2008.04.16 Jet Finder QA
- 2008.04.20 BUR 2009
- 2008.04.22 Run 6 Photon Yield Per Trigger
- 2008.05.07 Number of Jets
- 2008.05.09 Gamma-jets pT distributions
- 2008.05.19 Binning the shower shape library
- 2008.06.03 Jet A_LL Systematics
- 2008.06.18 Photon-jet reconstruction with the EEMC - Part 2 (STAR Collaboration Meeting - UC Davis)
- 2008.07.16 Extracting A_LL and DeltaG
- 2008.07.20 How to install Pythia 6 and 8 on your laptop?
- 2008.07.23 Hot Strips Identified by Hal Spinka
- 2008.07.24 Strips from Weihong's 2006 ppLong 20 runs
- G/h Discrimination Algorithm (Willie)
- Neutral Pions 2005: Frank Simon
- Neutral strange particle transverse asymmetries (tpb)
- Photon-jet with the Endcap (Ilya Selyuzhenkov)
- Relative Luminosity Analysis
- Run 6 Dijet Cross Section (Tai Sakuma)
- Run 6 Dijet Double Longitudinal Spin Asymmetry (Tai Sakuma)
- Run 6 Inclusive Jet Cross Section (Tai Sakuma)
- Run 6 Neutral Pions
- Run 6 Relative Luminosity (Tai Sakuma)
- Run 8 trigger planning (Jim Sowinski)
- Run 9
- Beam Polarizations
- Charged Pions
- Fully Reconstructed Ws
- Jet Trees
- W 2009 analysis , pp 500 GeV
- W 2011 AL
- W 2012 AL (begins here)
- W/Z 2013 Analysis
- Useful Links
- Weekly PWG Meetings
- Working Group Members
- Yearly Tasks
2007.05.30 Efficiency of reconstructing photons in EEMC
Updated on Fri, 2010-07-16 11:08. Originally created by seluzhen on 2010-07-16 10:26.
Under:
Pibero Djawotho Last updated Wed May 30 00:32:16 EDT 2007
Efficiency of reconstructing photons in EEMC
Monte Carlo sample
- 10k photons
- STAR y2006 geometry
- z-vertex=0
- Flat in pt 10-30 GeV
- Flat in eta 1.0-2.1
SMD gamma/pi0 discrimination algorithm
The following
from the IUCF STAR Web site gives a brief overview of the SMD gamma/pi0 discrimination algorithm using the method of maximal sided fit residual (data - fit). This technique comes to STAR EEMC from the Tevatron via Les Bland via Jason Webb. The specific fit function used in this analysis is:
f(x)=[0]*(0.69*exp(-0.5*((x-[1])/0.87)**2)/(sqrt(2*pi)*0.87)+0.31*exp(-0.5*((x-[1])/3.3)**2)/(sqrt(2*pi)*3.3))
x is the strip id in the SMD-u or SMD-v plane. The widths of the narrow and wide Gaussians are determined from empirical fits of shower shape response in the EEMC from simulation.
Optimizing cuts for gamma/pi0 separation
In the rest of this analysis, only those photons which have reconstructed pt > 5 GeV are kept. There is no requirement that the photon doesn't convert. The dividing curve between photons and pions is:
f(x)=4*x+1e-7*x**5
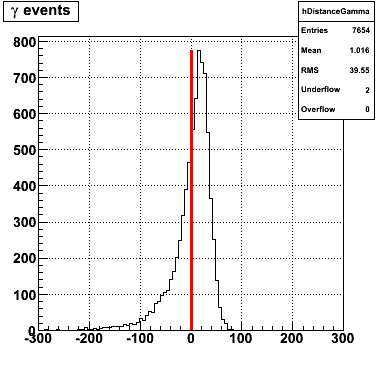
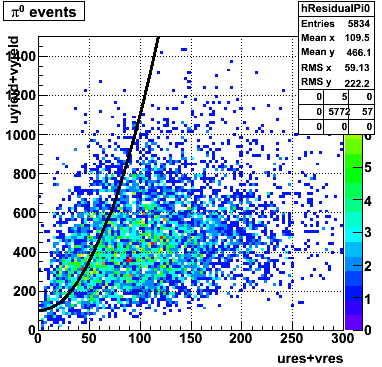
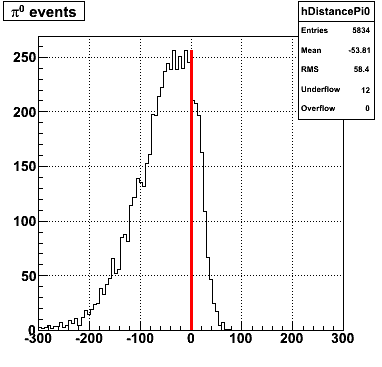
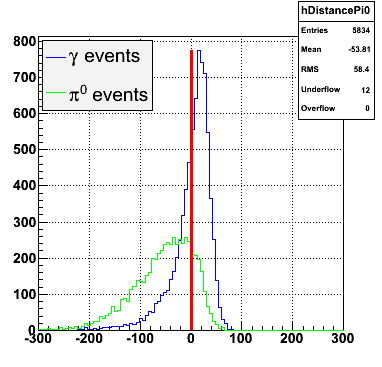
The y-axis is integrated yield over the SMD-u and SMD-v plane, and the x-axis is the sum of the maximal sided residual of the SMD-u and SMD-v plane.
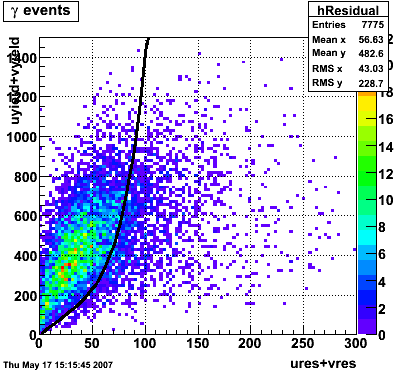 |
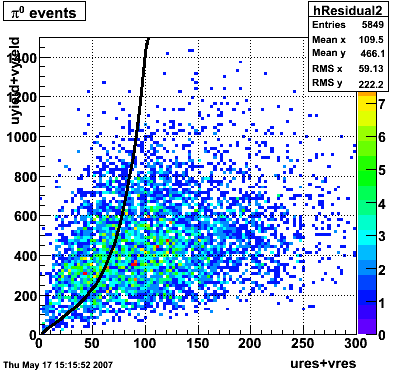 |
Following exchanges with Scott Wissink, the idea is to move from a quintic to a quadratic to reduce the number of parameters. In addition, the perpendicular distance between the curve and a point in the plane is used to estimate the likelihood of a particle being a photon or pion. Distances above the curve are positive and those below are negative. The more positive the distance, the more likely the particle is a photon. The more negative the distance, the more likely the particle is a pion.
Hi Pibero, With your new "linear plus quintic" curve (!) ... how did you choose the coefficients for each term? Or even the form of the curve? I'm not being picky, but how to optimize such curves will be an important issue as we (hopefully soon) move on to quantitative comparisons of efficiency vs purity. As a teaser, please see attached - small loss of efficiency, larger gain in purity. Scott
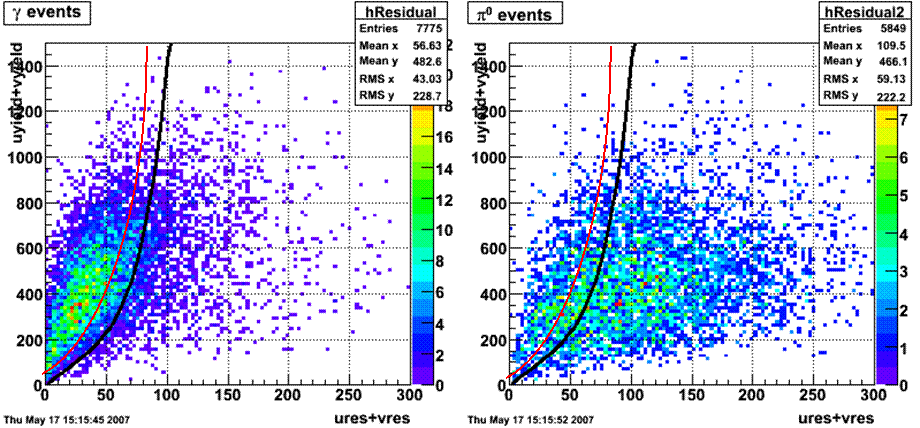
Hi Pibero,
I just worked out the distance of closest approach to a curve of the form
y(x) = a + bx^2
and it involves solving a cubic equation - so maybe not so trivial after
all. But if you want to pursue this (not sure it is your highest
priority right now!), the cubic could be solved numerically and "alpha"
could be easily calculated.
More fun and games.
Scott
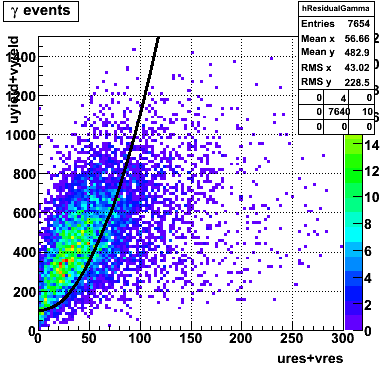 |
 |
 |
 |
 |
 |
Hi Pibero,
I played around with the equations a bit more, and I worked out an
analytic solution. But a numerical solution may still be better, since
it allows more flexibility in the algebraic form of the 'boundary' line
between photons and pions.
Here's the basic idea: suppose the curved line that cuts between
photons and pions can be expressed as y = f(x). If we are now given a
point (x0,y0) in the plane, our goal is to find the shortest distance to
this line. We can call this distance d (I think on your blackboard we
called it alpha).
To find the shortest distance, we need a straight line that passes
through (x0,y0) and is also perpendicular to the curve f(x). Let's
define the point where this straight line intersects the curve as
(x1,y1). This means (comparing slopes)
(y1 - y0) / (x1 - x0) = -1 / f'(x1)
where f'(x1) is the derivative of f(x) evaluated at the point (x1,y1).
Rearranging this, and using y1 = f(x1), yields the general result
f(x1) f'(x1) - y0 f'(x1) + x1 - x0 = 0
So, given f(x) and the point (x0,y0), the above is an equation in only
x1. Solve for x1, use y1 = f(x1), and then the distance d of interest
is given by
d = sqrt[ (x1 - x0)^2 + (y1 - y0)^2 ]
Example: suppose we got a reasonable separation of photons and pions
using a curve of the form
y = f(x) = a + bx^2
Using this in the above general equation yields the cubic equation
(2b^2) x1^3 + (2ab + 1 - 2by0) x1 - x0 = 0
Dividing through by 2b^2, we have an equation of the form
x^3 + px + q = 0
This can actually be solved analytically - but as I mentioned, a
numerical approach gives us more flexibility to try other forms for the
curve, so this may be the way to go. I think (haven't proved
rigorously) that for positive values of the constants a, b, x0, and y0,
the cubic will yield three real solutions for x1, but only one will have
x1 > 0, which is the solution of interest.
Anyway, it has been an interesting intellectual exercise!
Scott
I made use of the ROOT function TMath::RootsCubic to solve the cubic equation numerically for computing distances of each point to the curve. With the new quadratic curve f(x)=100+0.1*x^2 the efficiency is 63% and the rejection is 82%.
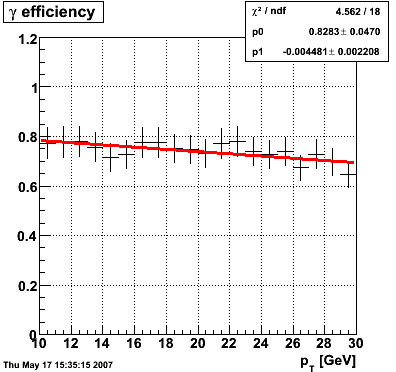
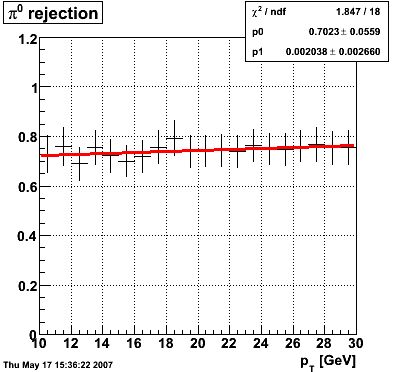
Efficiency and Rejection
The plot on the left below shows the efficiency of identifying photons over the pt range of 10-30 GeV and the one on the right shows the rejection rate of single neutral pions. Both average about 75% over the pt range of interest.
 |
 |
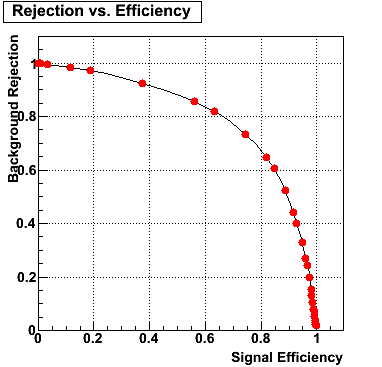
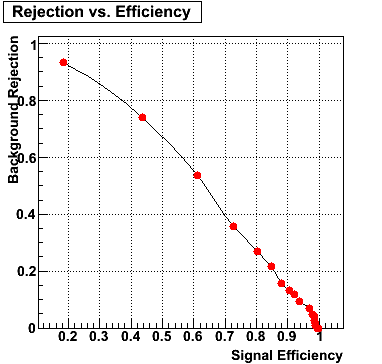
Rejection vs. efficiency at different energies
The plot below shows background rejection vs. signal efficiency for different energy ranges of the thrown gamma/pi0.

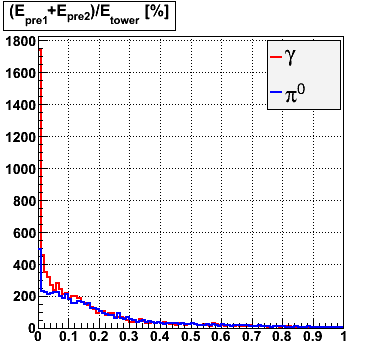
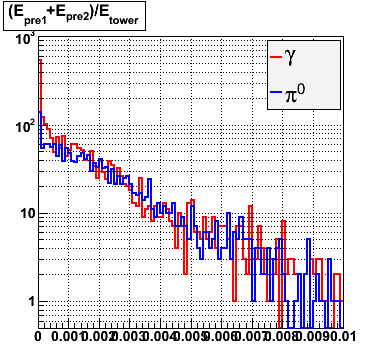
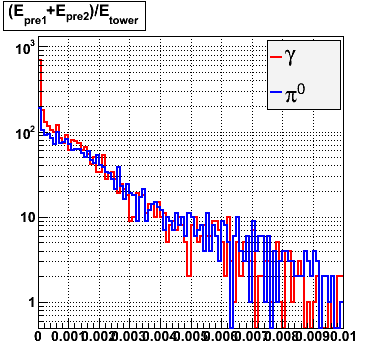
Rejection vs. efficiency with preshower cut
Below on the left is a plot of the ratio of the sum of preshower 1 and 2 to tower energy for both photons (red) and pions (blue). On the right is the rejection of pions vs. efficiency of photons as I cut on the ratio of preshower to tower. It is clear from these plots that the preshower layer is not a good gamma/pi0 discriminator, although can be used to add marginal improvement to the separation preovided by the shower max.
ALL ENERGIES |
|
 |
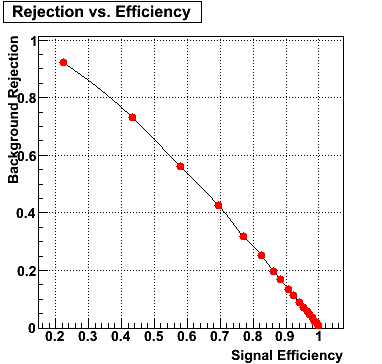 |
E=20-40 GeV |
|
 |
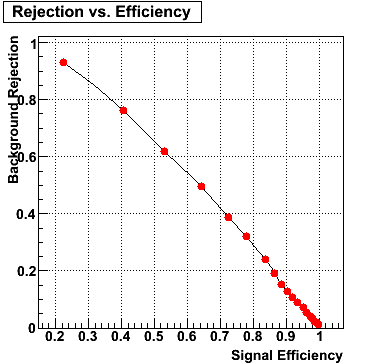 |
E=40-60 GeV |
|
 |
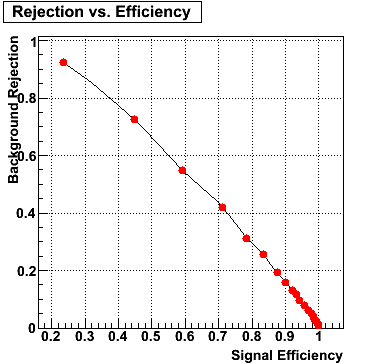 |
E=60-80 GeV |
|
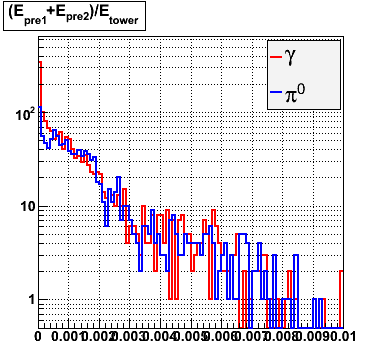 |
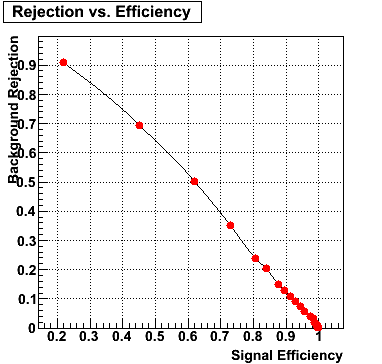 |
E=80-90 GeV |
|
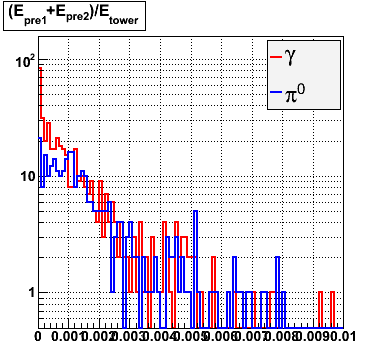 |
 |
Pibero Djawotho Last updated Wed May 30 00:32:16 EDT 2007
»
- Printer-friendly version
- Login or register to post comments
